题目内容
11.如图,在平行四边形ABCD中,AP⊥BD于点P,且$\overrightarrow{AP}$•$\overrightarrow{AC}$=18,则AP=3.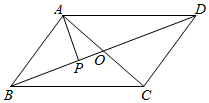
分析 可设AC,BD交于O点,AP⊥BD,从而在Rt△APO中,$|\overrightarrow{AO}|cos∠PAO=|\overrightarrow{AP}|$,从而便可得出$\overrightarrow{AP}•\overrightarrow{AC}=2|\overrightarrow{AP}{|}^{2}=18$,这样即可得出AP的值.
解答 解:如图,设AC,BD交于O点,∵AP⊥BD,则:
$\overrightarrow{AP}•\overrightarrow{AC}=|\overrightarrow{AP}||\overrightarrow{AC}|cos∠PAO$=$2|\overrightarrow{AP}||\overrightarrow{AO}|cos∠PAO=2|\overrightarrow{AP}{|}^{2}=18$;
∴AP=3.
故答案为:3.
点评 考查余弦函数的定义,平行四边形的对角线互相平分,以及向量数量积的计算公式.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
1.等差数列{an}的公差为3,若a2,a4,a8成等比数列,则{an}的前2n项S2n=( )
| A. | 3n(2n-1) | B. | 3n(2n+1) | C. | $\frac{3n(n+1)}{2}$ | D. | $\frac{3n(n-1)}{2}$ |
6.设等比数列{an}的前n项和为Sn,若S5、S4、S6成等差数列.则数列{an}的公比为q的值等于( )
| A. | -2或1 | B. | -1或2 | C. | -2 | D. | 1 |
16.已知实数x,y满足$\left\{\begin{array}{l}{x+y≥2}\\{x+2y≥3}\\{x≥0}\\{y≥0}\end{array}\right.$,则x+3y的最小值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
20.已知a>0,b>0,$a+b=\frac{1}{a}+\frac{1}{b}$,则$\frac{1}{a}+\frac{2}{b}$的最小值为( )
| A. | 4 | B. | $2\sqrt{2}$ | C. | 8 | D. | 16 |
1.集合P={x|x≥3或x≤-3},Q={y|y>-1},则P∩Q=( )
| A. | [3,+∞) | B. | (-∞,-3]∪(-1,+∞) | C. | (-1,+∞) | D. | (-∞,-1)∪[3,+∞) |