题目内容
1．集合P={x|x≥3或x≤-3}，Q={y|y＞-1}，则P∩Q=（ ）| A． | [3，+∞） | B． | （-∞，-3]∪（-1，+∞） | C． | （-1，+∞） | D． | （-∞，-1）∪[3，+∞） |
分析 由P与Q，求出两集合的交集即可．
解答 解：∵P=（-∞，-3]∪[3，+∞），Q=（-1，+∞），
∴P∩Q=[3，+∞），
故选：A．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12．已知f（x）=|x-2|+|x+1|+2|x+2|．
（1）求证：f（x）≥5；
（2）若对任意实数x，15-2f（x）＜a2+$\frac{9}{{{a^2}+1}}$都成立，求实数a的取值范围．
（1）求证：f（x）≥5；
（2）若对任意实数x，15-2f（x）＜a2+$\frac{9}{{{a^2}+1}}$都成立，求实数a的取值范围．
16．在△ABC中，内角A，B，C所对的边分别为a，b，c，若cos2B+cosB=1-cosAcosC，则（ ）
| A． | a、b、c 成等差数列 | B． | a、b、c成等比数列 | ||
| C． | a、2b、3c 成等差数列 | D． | a、2b、3c成等比数列 |
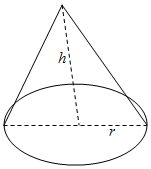如图，某边路清扫机构为预备融化道路积雪，需要在冬天储备$\frac{500}{3}$π（m3）的工业食盐，其食盐堆成底面半径为r（m），高为h（m）的圆锥，并用防水材料S（m2）遮蔽食盐（不考虑接缝与重叠，即面积与圆锥侧面积相同）