题目内容
4.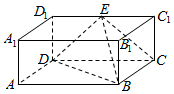 如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,AB=2a,E为C1D1的中点.
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,AB=2a,E为C1D1的中点.(1)求证:DE⊥平面BEC;
(2)求三棱锥C-BED的体积.
分析 (1)由六面体ABCD-A1B1C1D1为长方体,可得BC⊥侧面CDD1C1,得到DE⊥BC,在△CDE中,由勾股定理证得DE⊥EC,再由线面垂直的判定得答案;
(2)把三棱锥C-BED的体积转化为三棱锥D-BCE的体积求解.
解答 (1)证明:如图,∵BC⊥侧面CDD1C1,DE?侧面CDD1C1,
又DE?侧面CDD1C1,∴DE⊥BC,
在△CDE中,由已知得$CD=2a,CE=DE=\sqrt{2}a$,
则有CD2=CE2+DE2,
∴∠DEC=90°,即DE⊥EC,
又∵BC∩EC=C,∴DE⊥平面BCE;
(2)∵BC⊥侧面CDD1C1且CE?侧面CDD1C1,
∴CE⊥BC,
则${S_{△BCE}}=\frac{1}{2}•BC•CE=\frac{1}{2}×a×\sqrt{2}a=\frac{{\sqrt{2}}}{2}{a^2}$,
又∵DE⊥平面BCE,∴DE就是三棱锥D-BCE的高,
则${V_{C-BED}}={V_{E-BCD}}={V_{D-BCE}}=\frac{1}{3}•DE•{S_{△BCE}}=\frac{1}{3}×\sqrt{2}a×\frac{{\sqrt{2}}}{2}a=\frac{a^2}{3}$.
点评 本题考查直线与平面垂直的判定,考查了棱柱、棱锥及棱台体积的求法,训练了等积法,是中档题.

练习册系列答案
相关题目
18.若复数x满足(3+4i)x=|4+3i|,则x的虚部为( )
| A. | $\frac{4}{5}$ | B. | -4 | C. | -$\frac{4}{5}$ | D. | 4 |
15.设向量$\overrightarrow{AB}$=(3,4),$\overrightarrow{BC}$=(-2,-1),则cos∠BAC等于( )
| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
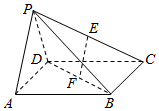 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,平面PAD⊥平面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD.
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,平面PAD⊥平面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD.