题目内容
在对人们休闲方式的一次调查中,得到数据如表:
为了检验休闲方式是否与性别有关系,根据表中数据得:
k=
≈6.201.
给出下列命题:
①至少有97.5%的把握认为休闲方式与性别有关.
②最多有97.5%的把握认为休闲方式与性别有关.
③在犯错误的概率不超过0.025的前提下认为休闲方式与性别有关系.
④在犯错误的概率不超过0.025的前提下认为休闲方式与性别无关.
其中的真命题是( )
| 休闲方式 性别 |
看电视 | 运动 | 合计 |
| 女 | 43 | 27 | 70 |
| 男 | 21 | 33 | 54 |
| 合计 | 64 | 60 | 124 |
k=
| 124(43×33-27×21)2 |
| 70×54×64×60 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 |
| k0 | 3.841 | 5.024 | 6.635 |
①至少有97.5%的把握认为休闲方式与性别有关.
②最多有97.5%的把握认为休闲方式与性别有关.
③在犯错误的概率不超过0.025的前提下认为休闲方式与性别有关系.
④在犯错误的概率不超过0.025的前提下认为休闲方式与性别无关.
其中的真命题是( )
| A、①③ | B、①④ | C、②③ | D、②④ |
考点:独立性检验
专题:阅读型
分析:根据临界值表判断假设不合理的程度,即可得“休闲方式与性别”有关的可靠性程度与犯错误的概率.
解答:
解:由列联表得:K2=
≈6.201>5.024,
∴至少有97.5%的把握认为“休闲方式与性别”有关,
即在犯错误的概率不超过0.025的前提下认为:“休闲方式与性别”有关.
故①③正确.
故选:A.
| 124(43×33-27×21)2 |
| 70×54×64×60 |
∴至少有97.5%的把握认为“休闲方式与性别”有关,
即在犯错误的概率不超过0.025的前提下认为:“休闲方式与性别”有关.
故①③正确.
故选:A.
点评:本题是一个独立性检验,我们可以利用临界值的大小来决定是否拒绝原来的统计假设,若值较大就拒绝假设,即拒绝两个事件无关.

练习册系列答案
相关题目
已知:集合P={x|x=sin
,k∈Z},集合Q={y|y=sin
,k∈Z},则P与Q的关系是( )
| (k-3)π |
| 3 |
| (-21-k)π |
| 3 |
| A、P?Q | B、P?Q |
| C、P=Q | D、P∩Q=∅ |
 已知定义在R上的函数f(x),其导函数y=f′(x)的大致图象如图所示,则下列叙述正确的是( )
已知定义在R上的函数f(x),其导函数y=f′(x)的大致图象如图所示,则下列叙述正确的是( )| A、f(a)取得极小值 |
| B、f(d)取得最小值 |
| C、f(x)在(a,c)上单调递增 |
| D、f(e)取得极大值 |
直线
(t为参数)与曲线ρ=1的位置关系是( )
|
| A、相离 | B、相交 | C、相切 | D、不确定 |
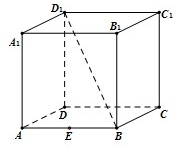 正方体AC1中,E为AB的中点,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PE⊥BD1,则动点P的轨迹是( )
正方体AC1中,E为AB的中点,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PE⊥BD1,则动点P的轨迹是( )| A、直线 | B、线段 |
| C、圆的一部分 | D、椭圆的一部分 |
函数f(x)=sin(4x+φ),x∈[0,2π]的一个零点为
,则f(x)的所有极值点的和为( )
| π |
| 8 |
| A、7π | ||
B、
| ||
C、
| ||
| D、9π |
函数f(x)=x2-x的零点个数是( )
| A、3 | B、2 | C、1 | D、0 |
