题目内容
两圆x2+y2-8x+6y-11=0和x2+y2=100的位置关系．
| A、相离 | B、相交 | C、外切 | D、内切 |
考点：圆与圆的位置关系及其判定
专题：计算题,直线与圆
分析：求出两圆的圆心坐标和两个半径R和r，然后利用两点间的距离公式求出两圆心的距离d，比较d与R-r及d与R+r的大小，即可得到两圆的位置关系．
解答：
解：x2+y2-8x+6y-11=0化为（x-4）2+（y+3）2=36，又x2+y2=100，
所以两圆心的坐标分别为：（4，-3）和（0，0），两半径分别为R=6和r=10，
则两圆心之间的距离d=5，
因为10-6＜5＜10+6，即R-r＜d＜R+r，所以两圆的位置关系是相交．
故选D．
所以两圆心的坐标分别为：（4，-3）和（0，0），两半径分别为R=6和r=10，
则两圆心之间的距离d=5，
因为10-6＜5＜10+6，即R-r＜d＜R+r，所以两圆的位置关系是相交．
故选D．
点评：此题考查学生掌握两圆的位置关系的判别方法，利用运用两点间的距离公式化简求值，是一道综合题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
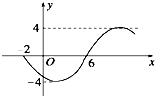函数f（x）=Asin（ωx+φ），（A＞0，ω＞0，x∈R）的部分图象如右图所示，则函数的表达式为（ ）A、f（x）=4sin（
| ||||
B、f（x）=4sin（
| ||||
C、f（x）=4sin（
| ||||
D、f（x）=4sin（
|
设a，b∈R，则“（a-b）a2＞0”是“a＞b”的（ ）
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、既不充分也不必要条件 |
| D、充要条件 |
已知x与y之间的一组数据，则y与x的线性回归方程
=
x+
必过点（ ）
 |
| y |
|
| b |
|
| a |
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| A、（2，2） |
| B、（1，2） |
| C、（1.5，4） |
| D、（1.5，0） |