题目内容
7.已知f'(x)为f(x)的导函数,若f(x)=ln$\frac{x}{2}$,且b$\int_1^b$$\frac{1}{x^3}$dx=2f'(a)+$\frac{1}{2}b}$-1,则a+b的最小值为( )| A. | $4\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $\frac{9}{2}$ | D. | $\frac{9}{2}+2\sqrt{2}$ |
分析 首先由已知的等式得到a,b的关系式,将所求转化为利用基本不等式求最小值.
解答 解:由b$\int_1^b$$\frac{1}{x^3}$dx=2f'(a)+$\frac{1}{2}b}$-1,得到b(-$\frac{1}{2}$x-2)|${\;}_{1}^{b}$=$\frac{4}{a}$+$\frac{1}{2}b}$-1,即$\frac{2}{a}+\frac{1}{2b}$=1,且a,b>0,
所以a+b=(a+b)($\frac{2}{a}+\frac{1}{2b}$)=$\frac{5}{2}+\frac{2b}{a}+\frac{a}{2b}$$≥\frac{9}{2}$;当且仅当$\frac{2b}{a}=\frac{a}{2b}$时等号成立;
故选C
点评 本题考查了定积分、导数的计算依据利用基本不等式求代数式的最小值.

练习册系列答案
相关题目
17.下列说法错误的是( )
| A. | 若p:?x∈R,x2-x+1=0,则¬p:?x∈R,x2-x+1≠0 | |
| B. | “sinθ=$\frac{1}{2}$”是“θ=30°或150°”的充分不必要条件 | |
| C. | 命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0” | |
| D. | 已知p:?x∈R,cosx=1,q:?x∈R,x2-x+1>0,则“p∧(¬q)”为假命题 |
16. 随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚.车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题.某汽车销售公司作了一次抽样调查,并统计得出某款车的使用年限x与所支出的总费用y(万元)有如表的数据资料:
随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚.车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题.某汽车销售公司作了一次抽样调查,并统计得出某款车的使用年限x与所支出的总费用y(万元)有如表的数据资料:
(1)在给出的坐标系中做出散点图;
(2)求线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的$\widehat{a}$、$\widehat{b}$;
(3)估计使用年限为12年时,车的使用总费用是多少?
(最小二乘法求线性回归方程系数公式$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$).
 随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚.车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题.某汽车销售公司作了一次抽样调查,并统计得出某款车的使用年限x与所支出的总费用y(万元)有如表的数据资料:
随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚.车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题.某汽车销售公司作了一次抽样调查,并统计得出某款车的使用年限x与所支出的总费用y(万元)有如表的数据资料:| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 总费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(2)求线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的$\widehat{a}$、$\widehat{b}$;
(3)估计使用年限为12年时,车的使用总费用是多少?
(最小二乘法求线性回归方程系数公式$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$).
 如图,在直角梯形ABCD中,∠DAB=∠CBA=90°,∠DCB=60°,AD=1,AB=$\sqrt{3}$,在直角梯形内挖去一个以A为圆心,以AD为半径的四分之一圆,得到图中阴影部分,求图中阴影部分绕直线AB旋转一周所得旋转体的体积、表面积.
如图,在直角梯形ABCD中,∠DAB=∠CBA=90°,∠DCB=60°,AD=1,AB=$\sqrt{3}$,在直角梯形内挖去一个以A为圆心,以AD为半径的四分之一圆,得到图中阴影部分,求图中阴影部分绕直线AB旋转一周所得旋转体的体积、表面积.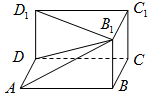 长方体ABCD-A1B1C1D1被挖去一个四棱锥后如图所示.已知AB=5,BC=4,BB=3.
长方体ABCD-A1B1C1D1被挖去一个四棱锥后如图所示.已知AB=5,BC=4,BB=3.