题目内容
9．已知直线x-2y-2k=0与两坐标轴围成的三角形面积不大于1，则实数k的取值范围是[-1，0）∪（0，1]．分析 先求出直线在两坐标轴上的截距，把三角形的面积表示出来，再根据其面积不大于1，建立关于k的不等式求解，注意去掉k=0时的情况．
解答 解：令x=0，得y=k；令y=0，得x=-2k．
∴三角形面积S=$\frac{1}{2}$|xy|=k2．
又S≤1，即k2≤1，
∴-1≤k≤1．
又当k=0时，直线过原点构不成三角形，故应舍去，
故答案为：[-1，0）∪（0，1]
点评 本题考查直线的一般式方程，在求解时易忘记验证k=0时是一个须舍去的点，故本题是一个易错题
练习册系列答案
阅读快车系列答案
相关题目
20．若函数f（x）是奇函数，且有三个零点x1、x2、x3，则x1+x2+x3的值为（ ）
| A． | -1 | B． | 不确定 | C． | 3 | D． | 0 |
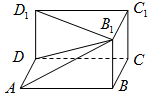长方体ABCD-A1B1C1D1被挖去一个四棱锥后如图所示．已知AB=5，BC=4，BB=3．
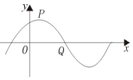已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的部分图象如图所示，其中点P（1，2）为函数图象的一个最高点，Q（4，0）为函数图象与x轴的一个交点，O为坐标原点．