Question

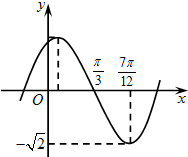函数f（x）=Asin（ωx+φ）（A，ω，φ为常数）的部分图象如图所示，则f（π）的值为

 

．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：由图象直接得到A和四分之一周期，结合周期公式求出ω，由五点作图的第三点求出φ，则函数解析式可求，取x=π求得f（π）的值．

解答： 解：由图可知：A=

2

，

T

4

=

7π

12

-

π

3

=

π

4

，
则T=π，ω=

2π

T

=

2π

π

=2．
由五点作图的第三点知：2×

π

3

+φ=

π

3

，解得φ=

π

6

．
∴f（x）=

2

sin（2x+

π

6

）．
则f（π）=

2

sin（2π+

π

6

）=

2

sin

π

6

=

2

×

1

2

=

2

2

．
故答案为：

2

2

．

点评：本题考查由Asin（ωx+φ）的部分图象求函数解析式，关键是正确利用五点作图的某一点求φ，是基础题．