题目内容
“ω=1”是“函数f(x)=sin2ωx-cos2ωx的最小正周期为π”的( )
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分又必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:三角函数的图像与性质,简易逻辑
分析:根据三角函数的图象和性质,结合充分条件和必要条件的定义进行判断即可得到结论.
解答:
解:f(x)=sin2ωx-cos2ωx=-cos2ωx,
当ω=1时,函数的周期T=
=π,∴充分性成立.
若函数f(x)=sin2ωx-cos2ωx的最小正周期为π,则T=
=π,
解得ω=±1,∴必要性不成立.
故“ω=1”是“函数f(x)=sin2ωx-cos2ωx的最小正周期为π”的充分不必要条件,
故选:B.
当ω=1时,函数的周期T=
| 2π |
| 2ω |
若函数f(x)=sin2ωx-cos2ωx的最小正周期为π,则T=
| 2π |
| |2ω| |
解得ω=±1,∴必要性不成立.
故“ω=1”是“函数f(x)=sin2ωx-cos2ωx的最小正周期为π”的充分不必要条件,
故选:B.
点评:本题主要考查充分条件和必要条件的判断,利用三角函数的周期性是解决本题的关键.

练习册系列答案
相关题目
若如图所示的程序框图输出的S是62,则在判断框中M表示的“条件”应该是( )


| A、n≥3 | B、n≥4 |
| C、n≥5 | D、n≥6 |
抛物线y2=2px的焦点与椭圆
+
=1的左焦点重合,则p的值为( )
| x2 |
| 25 |
| y2 |
| 16 |
| A、6 | B、-6 | C、-4 | D、4 |
执行如图所示的程序框图,则输出的a的值为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
如果执行所示的程序框图,那么输出的S为( )


| A、96 | B、768 |
| C、1536 | D、768 |
在△ABC中,角A,B,C所对的边分别是a,b,c,若
=
,则△ABC的形状是( )
| a |
| cosA |
| c |
| cosC |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰或直角三角形 |
已知数列{an}的通项公式为an=3n-2(n∈N+),则a3+a6+a9+a12+a15=( )
| A、120 | B、125 |
| C、130 | D、135 |
执行下边的程序框图,则输出的n是( )


| A、4 | B、5 | C、6 | D、7 |
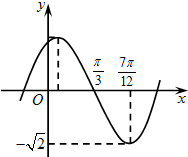 函数f(x)=Asin(ωx+φ)(A,ω,φ为常数)的部分图象如图所示,则f(π)的值为
函数f(x)=Asin(ωx+φ)(A,ω,φ为常数)的部分图象如图所示,则f(π)的值为