题目内容
设f(x)是定义在R上的奇函数,已知f(x+4)=-f(x),且f(3)=5,则f(-21)= ,f(2011)= .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据条件f(x+4)=-f(x),得到函数是周期为8的周期函数,利用函数的周期性即可得到结论.
解答:
解:由f(x+4)=-f(x),
得f(x+8)=-f(x+4)=f(x),
∴函数的周期是8,
∵f(3)=5,
∴f(-21)=f(-21+24)=f(3)=5,
f(2011)=f(251×8+3)=f(3)=5,
故答案为:5,5
得f(x+8)=-f(x+4)=f(x),
∴函数的周期是8,
∵f(3)=5,
∴f(-21)=f(-21+24)=f(3)=5,
f(2011)=f(251×8+3)=f(3)=5,
故答案为:5,5
点评:本题主要考查函数值的计算,根据条件得到函数是周期是8的周期函数是解决本题的关键.

练习册系列答案
相关题目
复数z=
-(i-1)(i+1)的模是( )
| 1 |
| i |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
已知首项为1的等比数列{an}是摆动数列,Sn是{an}的前n项和,且
=5,则数列{
}的前5项和为( )
| S4 |
| S2 |
| 1 |
| an |
| A、31 | ||
B、
| ||
C、
| ||
| D、11 |
 如图是求10!的程序框图,则在判断框内应填的条件可以是( )
如图是求10!的程序框图,则在判断框内应填的条件可以是( )| A、i<10? |
| B、i≤10? |
| C、i≤11? |
| D、i>10? |
如果执行所示的程序框图,那么输出的S为( )


| A、96 | B、768 |
| C、1536 | D、768 |
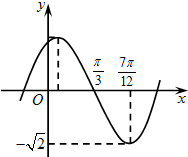 函数f(x)=Asin(ωx+φ)(A,ω,φ为常数)的部分图象如图所示,则f(π)的值为
函数f(x)=Asin(ωx+φ)(A,ω,φ为常数)的部分图象如图所示,则f(π)的值为