题目内容
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A、y=
| ||
B、y=(
| ||
| C、y=x(x∈R) | ||
| D、y=x3(x∈R) |
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:根据函数的奇偶性和单调性的判断方法,即可得到在其定义域内既是奇函数又是减函数的函数.
解答:
解:对于A.函数的定义域为{x|x≠0且x∈R},关于原点对称,f(-x)=f(x),则为偶函数,故A不满足;
对于B.定义域R关于原点对称,f(-x)≠-f(x)且≠f(x),则为非奇非偶函数,故B不满足;
对于C.y=x为奇函数,在R上是增函数,故C不满足;
对于D.定义域R关于原点对称,f(-x)=-(-x)3=-f(x),则为奇函数,y′=-3x2≤0,则为减函数,故D满足.
故选D.
对于B.定义域R关于原点对称,f(-x)≠-f(x)且≠f(x),则为非奇非偶函数,故B不满足;
对于C.y=x为奇函数,在R上是增函数,故C不满足;
对于D.定义域R关于原点对称,f(-x)=-(-x)3=-f(x),则为奇函数,y′=-3x2≤0,则为减函数,故D满足.
故选D.
点评:本题考查函数的奇偶性和单调性的判断,考查定义法和导数、及性质的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
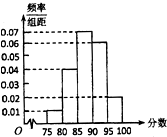 某次有1000人参加数学摸底考试,其成绩的频率分布直方图如题(16)图所示,规定85分及以上为优秀.
某次有1000人参加数学摸底考试,其成绩的频率分布直方图如题(16)图所示,规定85分及以上为优秀.
