题目内容
16.已知函数的定义域为R,且满足下列三个条件:①对任意的x1,x2∈[4,8],当x1<x2时,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0;
②f(x+4)=-f(x);
③y=f(x+4)是偶函数;
若a=f(6),b=f(11),c=f(2017),则a,b,c的大小关系正确的是( )
| A. | a<b<c | B. | b<a<c | C. | a<c<b | D. | c<b<a |
分析 根据题意,由①分析可得函数f(x)在区间[4,8]上为增函数,由②分析可得函数f(x)的周期为8,由③分析可得函数f(x)的图象关于直线x=-4和x=4对称,进而分析可得a=f(6),b=f(11)=f(3)=f(5),c=f(2017)=f(252×8+1)=f(1)=f(7),结合函数在[4,8]上的单调性,分析可得答案.
解答 解:根据题意,
若对任意的x1,x2∈[4,8],当x1<x2时,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,则函数f(x)在区间[4,8]上为增函数,
若f(x+4)=-f(x),则f(x+8)=-f(x+4)=f(x),即函数f(x)的周期为8,
若y=f(x+4)是偶函数,则函数f(x)的图象关于直线x=-4对称,又由函数的周期为8,则函数f(x)的图象也关于直线x=4对称,
a=f(6),b=f(11)=f(3)=f(5),c=f(2017)=f(252×8+1)=f(1)=f(7),
又由函数f(x)在区间[4,8]上为增函数,
则有b<a<c;
故选:B.
点评 本题考查抽象函数的应用,关键是依据题意,分析函数的单调性和周期性.

练习册系列答案
相关题目
6. 如图,已知正方体ABCD-A'B'C'D'的外接球的体积为$\frac{{\sqrt{3}}}{2}π$,将正方体割去部分后,剩余几何体的三视图如图所示,则剩余几何体的表面积为( )
如图,已知正方体ABCD-A'B'C'D'的外接球的体积为$\frac{{\sqrt{3}}}{2}π$,将正方体割去部分后,剩余几何体的三视图如图所示,则剩余几何体的表面积为( )
 如图,已知正方体ABCD-A'B'C'D'的外接球的体积为$\frac{{\sqrt{3}}}{2}π$,将正方体割去部分后,剩余几何体的三视图如图所示,则剩余几何体的表面积为( )
如图,已知正方体ABCD-A'B'C'D'的外接球的体积为$\frac{{\sqrt{3}}}{2}π$,将正方体割去部分后,剩余几何体的三视图如图所示,则剩余几何体的表面积为( )| A. | $\frac{9}{2}+\frac{{\sqrt{3}}}{2}$ | B. | $3+\sqrt{3}$或$\frac{9}{2}+\frac{{\sqrt{3}}}{2}$ | C. | $2+\sqrt{3}$ | D. | $\frac{9}{2}+\frac{{\sqrt{3}}}{2}$或$2+\sqrt{3}$ |
4.设α,β是两个不同的平面,l是直线且l?α,则“α∥β”是“l∥β”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
11.已知集合A={0,1,2},B={x|x2-5x+4<0},A∩(∁RB)=( )
| A. | {0,1,2} | B. | {1,2} | C. | {0} | D. | {0,1} |
1.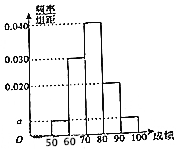 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
(Ⅰ)求图中a的值;
(Ⅱ)估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表);
(Ⅲ)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
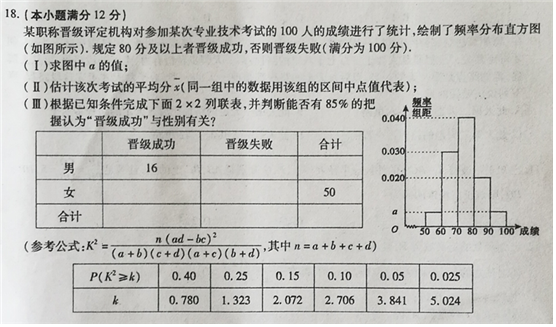
 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).(Ⅰ)求图中a的值;
(Ⅱ)估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表);
(Ⅲ)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | ||
| 女 | 50 | ||
| 合计 |
| P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |

8.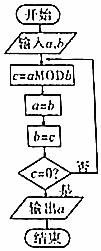 “欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )
“欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )
 “欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )
“欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )| A. | 0 | B. | 25 | C. | 50 | D. | 75 |
6.已知三个向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$共面,且均为单位向量,$\overrightarrow{a}$•$\overrightarrow{b}$=0,则|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|的取值范围是( )
| A. | [$\sqrt{2}$-1,$\sqrt{2}$+1] | B. | [1,$\sqrt{2}$] | C. | [$\sqrt{2}$,$\sqrt{3}$] | D. | [$\sqrt{2}$-1,1] |
 如图,在三棱锥ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1=4,A1在底面ABC上的射影为BC的中点E,D是B1C1的中点.
如图,在三棱锥ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1=4,A1在底面ABC上的射影为BC的中点E,D是B1C1的中点.