题目内容

7．若集合A={-1，2}，B={0，1}，则集合{z|z=x+y，x∈A，y∈B}中的元素的个数为（　　）
A．5B．4C．3D．2

分析 根据元素与集合的关系进行判断

解答 解：集合A={-1，2}，B={0，1}，
集合{z|z=x+y，x∈A，y∈B}，
当x=-1时，y=0，或1，可得z=-1或0，
当x=2时，y=0，或1，可得z=2或3，
那么构造集合z的元素有：-1，0，2，3．有4个元素．
故选B．

点评 本题主要考查元素与集合的关系，属于基础题．

练习册系列答案
相关题目
7．已知函数$f（x）=x-mlnx-\frac{m-1}{x}（{m∈R}）$，$g（x）=\frac{1}{2}{x^2}+{e^x}-x{e^x}$，
（1）当x∈[1，e]，求f（x）的最小值，
（2）当m≤2时，若存在${x_1}∈[{e，{e^2}}]$，使得对任意x2∈[-2，0]，f（x1）≤g（x2）成立，求实数m的取值范围．
18．已知命题p：“?x∈R时，都有${x^2}-x+\frac{1}{4}＞0$”； 命题q：“?x°∈R，使sinx°+cosx°=2时”，则下列判断正确的是（　　）
A．p∨q为假命题B．p∧q为真命题C．￢p∧q为真命题D．￢p∨￢q为假命题
15．茎叶图如图1，为高三某班60名学生的化学考试成绩，算法框图如图2中输入的a1为茎叶图中的学生成绩，则输出的m，n分别是（　　）
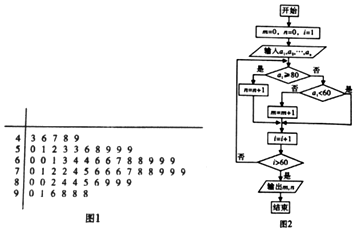
A．m=29，n=15B．m=29，n=16C．m=15，n=16D．m=16，n=15
2．为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分（十分制）如图所示，假设得分的中位数为me，众数为m0，平均值为$\overline x$，则（　　）
A．me=m0=$\overline x$B．me=m0＜$\overline x$C．me＜m0＜$\overline x$D．m0＜me＜$\overline x$
12．已知函数f（x）=x4cosx+mx2+2x（m∈R），若导函数f'（x）在区间[-4，4]上有最大值16，则导函数f'（x）在区间[-4，4]上的最小值为（　　）
A．-16B．-12C．12D．16
19．三棱锥P-ABC的底面ABC是等腰直角三角形，∠A=90°，侧面PAB是等边三角形且与底面ABC垂直，AB=6，则该三棱锥的外接球半径为$\frac{3\sqrt{7}}{2}$．
16．设双曲线C的焦点在x轴上，渐近线方程为$y=±\frac{{\sqrt{2}}}{2}x$，则其离心率为$\frac{\sqrt{6}}{2}$．
17．已知二项式（x-$\frac{a}{\root{3}{x}}$）4的展开式中常数项为32，则a=（　　）
A．8B．-8C．2D．-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网