题目内容
19.三棱锥P-ABC的底面ABC是等腰直角三角形,∠A=90°,侧面PAB是等边三角形且与底面ABC垂直,AB=6,则该三棱锥的外接球半径为$\frac{3\sqrt{7}}{2}$.分析 求出P到平面ABC的距离为3$\sqrt{3}$,可得球心O到平面ABC的距离,即可求出三棱锥的外接球半径.
解答 解:设球心O到平面ABC的距离为h,则
由P到平面ABC的距离为3$\sqrt{3}$,可得球心O到平面ABC的距离为h=$\frac{3\sqrt{3}}{2}$,
∴该三棱锥的外接球半径为$\sqrt{(\frac{3\sqrt{3}}{2})^{2}+{3}^{2}}$=$\frac{3\sqrt{7}}{2}$,
故答案为$\frac{3\sqrt{7}}{2}$.
点评 本题考查三棱锥的外接球半径,考查面面垂直,比较基础.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
4.设M{a,b,c}=$\left\{\begin{array}{l}{a,b,c的中位数,(a-b)(b-c)(c-a)≠0}\\{a,b,c的众数,(a-b)(b-c)(c-a)=0}\end{array}\right.$,若f(x)=M{2x,x2,4-7.5x}(x>0),则f(x)的最小值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{5}{4}$ |
9.已知a,b,c满足a>b>c,ac<0,则下列不等关系中正确的是( )
| A. | cb2<ab2 | B. | ab<ac | C. | c(a-c)>0 | D. | a+ac>b+ac |




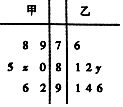 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是89.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是89.