题目内容
10.若θ∈[0,π],则$sin({θ+\frac{π}{3}})>\frac{1}{2}$成立的概率为$\frac{1}{2}$.分析 本题考查的知识点是几何概型的意义,关键是要找出sinθ>0对应线段的长度,再将其代入几何概型计算公式进行求解即得结果.
解答 解:θ∈[0,π],区间长度为π,
$sin({θ+\frac{π}{3}})>\frac{1}{2}$,$\frac{π}{6}$$<θ+\frac{π}{3}$<$\frac{5π}{6}$,∵θ∈[0,π],∴θ∈[0,$\frac{1}{2}$π],对应的区间长度为$\frac{1}{2}$π,
根据几何概型计算公式可得“$sin({θ+\frac{π}{3}})>\frac{1}{2}$”的概率是$\frac{1}{2}$.
故答案为:$\frac{1}{2}$
点评 几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
相关题目
20.如图为一个简单组合体的三视图,其中正视图由 一个半圆和一个正方形组成,则该组合体的表面积为( )
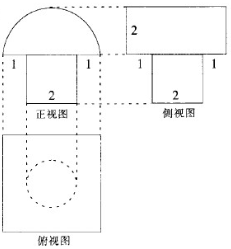

| A. | 20+17π | B. | 20+16π | C. | 16+17π | D. | 16+l6π |
5.学校某文具商店经营某种文具,商店每销售一件该文具可获利3元,若供大于求则削价处理,每处理一件文具亏损1元;若供不应求,则可以从外部调剂供应,此时每件文具仅获利2元.为了了解市场需求的情况,经销商统计了去年一年(52周)的销售情况.
以去年每周的销售量的频率为今年每周市场需求量的概率.
(1)要使进货量不超过市场需求量的概率大于0.5,问进货量的最大值是多少?
(2)如果今年的周进货量为14,平均来说今年每周的利润是多少?
| 销售量(件) | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 周数 | 2 | 4 | 8 | 13 | 13 | 8 | 4 |
(1)要使进货量不超过市场需求量的概率大于0.5,问进货量的最大值是多少?
(2)如果今年的周进货量为14,平均来说今年每周的利润是多少?
15.sin(-1740°)的值是( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
