题目内容
19.在△ABC中,$tanC=\frac{4}{3}$,$\overrightarrow{AH}•\overrightarrow{BC}=0$,$\overrightarrow{AB}•(\overrightarrow{CA}+\overrightarrow{CB})=0$,H在BC边上,则过点B以A、H为两焦点的双曲线的离心率为$\frac{\sqrt{5}+1}{2}$.分析 由△ABC中tanC=$\frac{4}{3}$,根据向量垂直的数量积为0,易得△ABC是等腰三角形,AH为腰上高,
由此设出各边的长度,然后根据双曲线的性质及双曲线离心率的定义,即可求出答案.
解答 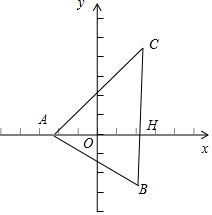 解:如图所示;
解:如图所示;
△ABC中,$\overrightarrow{AH}•\overrightarrow{BC}=0$,
∴AH为BC边上的高;
又$\overrightarrow{AB}•(\overrightarrow{CA}+\overrightarrow{CB})=0$,
∴CA=CB;
又tanC=$\frac{4}{3}$,令AH=4X,则CH=3X,
AC=CB=5X,BH=2X,
∴AB=$\sqrt{{(4X)}^{2}{+(2X)}^{2}}$=2$\sqrt{5}$X;
∴过点B以A、H为两焦点的双曲线中
2a=BA-BH=2($\sqrt{5}$-1)X,
2c=AH=4X;
∴过点B以A、H为两焦点的双曲线的离心率为
e=$\frac{c}{a}$=$\frac{4X}{2(\sqrt{5}-1)X}$=$\frac{\sqrt{5}+1}{2}$.
故答案为:$\frac{{\sqrt{5}+1}}{2}$.
点评 本题考查了双曲线的简单性质,根据已知求出满足条件的△ABC形状进而求出各边长是解答本题的关键.

练习册系列答案
相关题目
9.已知命题p:存在向量$\overrightarrow{a}$,$\overrightarrow{b}$,使得$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|,命题q:对任意的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,则$\overrightarrow{b}$=$\overrightarrow{c}$.则下列判断正确的是( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∨(¬q)是假命题 | D. | 命题p∧(¬q)是真命题 |
7.一个几何体的三视图及其尺寸如图所示,则该几何体的体积为( )


| A. | $\frac{28}{3}$ | B. | $\frac{{28\sqrt{2}}}{3}$ | C. | 28 | D. | $22+6\sqrt{3}$ |
4.设Sn是等差数列{an}的前n项和,a1=2,a5=3a3,则a3=( )
| A. | -2 | B. | 0 | C. | 3 | D. | 6 |
8.若函数f(x)=sinα-sinx,则f′(α)=( )
| A. | -sinα | B. | -cosα | C. | cosα-sinα | D. | sinα-cosα |
3.研究表明,成年人的身高和体重具有线性相关性,小明随机调查了五名成年人甲,乙,丙,丁,戊的身高和体重,得到的结果如下表所示
身高x和体重y的回归直线方程为y=$\frac{5}{4}$x+a,那么身高为180cm的成年人体重大约是73 kg.
| 编号 | 甲 | 乙 | 丙 | 丁 | 戊 |
| 身高x(cm) | 166 | 170 | 172 | 174 | 178 |
| 体重y(kg) | 55 | 60 | 65 | 65 | 70 |