题目内容
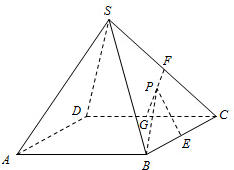 如图,正四棱锥S-ABCD中,SA=AB,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点.
如图,正四棱锥S-ABCD中,SA=AB,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点.(l)求证:EP⊥AC;
(2)当直线BP与平面EFG所成的角取得最大值时,求二面角P-BD-C的大小.
考点:二面角的平面角及求法,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(1)设AC交BD于O,则SO⊥底面ABCD,从而SO⊥AC,又BD⊥AC,从而AC⊥平面SBF,进而AC⊥SO,由此能证明PE⊥AC.
(2)设AB=2,建立空间直角坐标系,求出面EFG的法向量,设BP与平面EFG所成角为α,由向量法能求出点P在线段FG上,λ=1时sinα取最大值,由此能求出二面角P-BD-C的大小.
(2)设AB=2,建立空间直角坐标系,求出面EFG的法向量,设BP与平面EFG所成角为α,由向量法能求出点P在线段FG上,λ=1时sinα取最大值,由此能求出二面角P-BD-C的大小.
解答:
解:(1)证明:设AC交BD于O,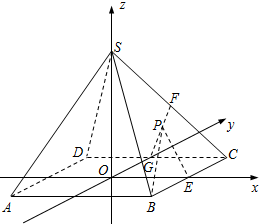
∵S-ABCD为正四棱锥,∴SO⊥底面ABCD,
∴SO⊥AC,(1分)又∵BD⊥AC,
∴AC⊥平面SBF,∴AC⊥SO,
∵SD∥FG,∴AC⊥GF,又AC⊥GE,∴AC⊥平面GEF,
又∵PE?面GEF,∴PE⊥AC.(4分)
(2)解:设AB=2,如图建立空间直角坐标系,
则G(0,1,0),E(1,0,0),C(1,1,0),
S(0,0,
),F(
,
,
),B(1,-1,0),
∴
=(
,-
,
),(5分)
设
=λ
=(
,-
,
λ),故点P(
,1-
,
λ)
∴
=(
-1,2-
,
λ),(6分)
设面EFG的法向量为
=(a,b,c),
∵n⊥
,n⊥
∴
,令a=1,得
=(1,1,0)(7分)
设BP与平面EFG所成角为α,
则sinα=
=
(8分)
∵点P在线段FG上,∴0≤λ≤1,即λ=1时sinα取最大值
此时点P与点F重合(9分)
设二面角P-BD-C的大小为θ
∵点P到平面ABCD的距离为
,点P到BD的距离为1(10分)
则sinθ=
=
∴二面角P-BD-C的大小为45°.(12分)

∵S-ABCD为正四棱锥,∴SO⊥底面ABCD,
∴SO⊥AC,(1分)又∵BD⊥AC,
∴AC⊥平面SBF,∴AC⊥SO,
∵SD∥FG,∴AC⊥GF,又AC⊥GE,∴AC⊥平面GEF,
又∵PE?面GEF,∴PE⊥AC.(4分)
(2)解:设AB=2,如图建立空间直角坐标系,
则G(0,1,0),E(1,0,0),C(1,1,0),
S(0,0,
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴
| GF |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
设
| GP |
| GF |
| λ |
| 2 |
| λ |
| 2 |
| ||
| 2 |
| λ |
| 2 |
| λ |
| 2 |
| ||
| 2 |
∴
| BP |
| λ |
| 2 |
| λ |
| 2 |
| ||
| 2 |
设面EFG的法向量为
| n |
∵n⊥
| EF |
| GE |
∴
|
| n |
设BP与平面EFG所成角为α,
则sinα=
|
| ||||||||||
|
| ||
| 2 |
| 1 | ||
|
∵点P在线段FG上,∴0≤λ≤1,即λ=1时sinα取最大值
此时点P与点F重合(9分)
设二面角P-BD-C的大小为θ
∵点P到平面ABCD的距离为
| ||
| 2 |
则sinθ=
| ||||
| 1 |
| ||
| 2 |
∴二面角P-BD-C的大小为45°.(12分)
点评:本题考查线面垂直的证明,考查线面角最大时二面角的求法,是中档题,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
i是虚数单位,
的共轭复数为( )
| 2i |
| 1+i |
| A、-1+i | B、1+i |
| C、-1-i | D、1-i |
过抛物线y2=4x焦点作直线L与抛物线交于A、B,过A、B分别作抛物线的切线交于点P,则△ABP为( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、随P位置变化前三种情况都有可能 |
如图是一容量为100的样本的重量的频率分布直方图,则由图可估计样本的平均重量为( )

| A、13 | B、12 | C、11 | D、10 |
