题目内容
某小区在一次对20岁以上居民节能意识的问卷调查中,随机抽取了100份问卷进行统计,得到相关的数据如下表:
(1)由表中数据直观分析,节能意识强弱是否与人的年龄有关?
(2)若全小区节能意识强的人共有350人,则估计这350人中,年龄大于50岁的有多少人?
(3)按年龄分层抽样,从节能意识强的居民中抽5人,再是这5人中任取2人,求恰有1人年龄在20至50岁的概率.
| 节能意识弱 | 节能意识强 | 总计 | |
| 20至50岁 | 45 | 9 | 54 |
| 大于50岁 | 10 | 36 | 46 |
| 总计 | 55 | 45 | 100 |
(2)若全小区节能意识强的人共有350人,则估计这350人中,年龄大于50岁的有多少人?
(3)按年龄分层抽样,从节能意识强的居民中抽5人,再是这5人中任取2人,求恰有1人年龄在20至50岁的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)利用独立性检验的基本思想,只要在每个年龄段计算它们节能意识强的概率,若差距较大说明与年龄有关,也可利用|ad-bc|的值的大小来直观判断;
(2)先利用统计数据计算在节能意识强的人中,年龄大于50岁的概率,再由总体乘以概率即可得总体中年龄大于50岁的有多少人;
(3)先确定抽样比,即每层中应抽取
,故再抽到的5人中,一人年龄小于50,4人年龄大于50,从中取两个,求恰有1人年龄在20至50岁的概率为古典概型,利用古典概型的概率计算公式,分别利用列举法计数即可得所求概率
(2)先利用统计数据计算在节能意识强的人中,年龄大于50岁的概率,再由总体乘以概率即可得总体中年龄大于50岁的有多少人;
(3)先确定抽样比,即每层中应抽取
| 1 |
| 9 |
解答:
解(1)因为20至50岁的54人有9人节能意识强,
大于50岁的46人有36人节能意识强,
与
相差较大,所以节能意识强弱与年龄有关;
(2)由数据可估计在节能意识强的人中,年龄大于50岁的概率约为
,
故年龄大于50岁的约有
×350=280(人);
(3)抽取节能意识强的5人中,年龄在20至50岁的有5×
=1人,
年龄大于50岁的有5-1=4人,记这5人分别为A,B1,B2,B3,B4.
从这5人中任取2人,所有可能情况有10种,列举如下:
(A,B1),(A,B2),(A,B3),(A,B4),(B1,B2),
(B1,B3),(B1,B4),(B2,B3),(B2,B4),(B3,B4),
设A表示事件“这5人中任取2人,恰有1人年龄在20岁至50岁”,
则A中的基本事件有(A,B1),(A,B2),(A,B3),(A,B4),共4种,
所以P(A)=
=
.
故所求概率为
.
大于50岁的46人有36人节能意识强,
| 9 |
| 54 |
| 36 |
| 46 |
(2)由数据可估计在节能意识强的人中,年龄大于50岁的概率约为
| 36 |
| 45 |
故年龄大于50岁的约有
| 36 |
| 45 |
(3)抽取节能意识强的5人中,年龄在20至50岁的有5×
| 9 |
| 45 |
年龄大于50岁的有5-1=4人,记这5人分别为A,B1,B2,B3,B4.
从这5人中任取2人,所有可能情况有10种,列举如下:
(A,B1),(A,B2),(A,B3),(A,B4),(B1,B2),
(B1,B3),(B1,B4),(B2,B3),(B2,B4),(B3,B4),
设A表示事件“这5人中任取2人,恰有1人年龄在20岁至50岁”,
则A中的基本事件有(A,B1),(A,B2),(A,B3),(A,B4),共4种,
所以P(A)=
| 4 |
| 10 |
| 2 |
| 5 |
故所求概率为
| 2 |
| 5 |
点评:本题考查独立性检验的基本思想,属基础题.

练习册系列答案
相关题目
已知f(x)=2sin(2x+
),若将它的图象向右平移
个单位,得到函数g(x)的图象,则函数g(x)图象的一条对称轴的方程为( )
| π |
| 6 |
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
若集合A={x|1gx<1},B={y|y=sinx,x∈R},则A∩B=( )
| A、(0,1) | B、(0,1] |
| C、[-1,1] | D、∅ |
函数f(x)=x2+mx+9在区间(-3,3)上具有单调性,则实数m的取值范围是( )
| A、(-∞,-6] |
| B、[6,+∞) |
| C、(-∞,-6]∪[6,+∞) |
| D、[-6,6] |
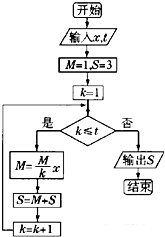 执行如图所示的程序框图,如果输入x,t的值均为2,最后输出S的值为n,在区间[0,10]上随机选取一个数D,则D≤n的概率为( )
执行如图所示的程序框图,如果输入x,t的值均为2,最后输出S的值为n,在区间[0,10]上随机选取一个数D,则D≤n的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
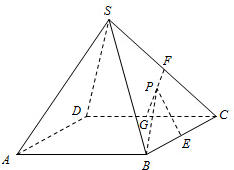 如图,正四棱锥S-ABCD中,SA=AB,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点.
如图,正四棱锥S-ABCD中,SA=AB,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点.