题目内容
解不等式:x2-(a+
)x+1>0.
| 1 |
| a |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:(x-a)(x-
)>0.对a分类讨论即可得出.
| 1 |
| a |
解答:
解:(x-a)(x-
)>0.
当a>1时,a>
,∴不等式的解集为{x|x>a或x<
};
当a=1时,不等式的解集为{x|x≠1};
当0<a<1时,a<
,∴不等式的解集为{x|x>
或x<a};
当-1<a<0时,a>
,∴不等式的解集为{x|x<
或x>a};
当a=-1时,∴不等式的解集为{x|x≠-1};
当a<-11时,a<
,∴不等式的解集为{x|x>
或x<a}.
| 1 |
| a |
当a>1时,a>
| 1 |
| a |
| 1 |
| a |
当a=1时,不等式的解集为{x|x≠1};
当0<a<1时,a<
| 1 |
| a |
| 1 |
| a |
当-1<a<0时,a>
| 1 |
| a |
| 1 |
| a |
当a=-1时,∴不等式的解集为{x|x≠-1};
当a<-11时,a<
| 1 |
| a |
| 1 |
| a |
点评:本题考查了一元二次不等式的解法、分类讨论思想方法,考查了计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
给定两个命题:
p:?a∈R,使y=x2+
为偶函数;
q:?x∈R,(sinx-1)(cosx-1)≥0恒成立.
其中正确的命题的为( )
p:?a∈R,使y=x2+
| a |
| x+1 |
q:?x∈R,(sinx-1)(cosx-1)≥0恒成立.
其中正确的命题的为( )
| A、p∧q | B、p∧¬q |
| C、p∨¬q | D、¬p∨q |
已知cosα=-
,α为三角形的内角,则tan(
-α)的值为( )
| 3 |
| 5 |
| 5π |
| 4 |
A、
| ||
B、-
| ||
| C、7 | ||
| D、-7 |
如果lgx+lgx2+…+lgx10=110,那么lgx+lg2x+…+lg10x=( )
| A、211-2 |
| B、211+2 |
| C、210+2 |
| D、210-2 |
若集合A={x|1gx<1},B={y|y=sinx,x∈R},则A∩B=( )
| A、(0,1) | B、(0,1] |
| C、[-1,1] | D、∅ |
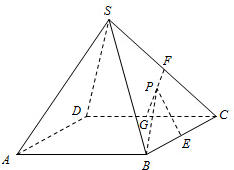 如图,正四棱锥S-ABCD中,SA=AB,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点.
如图,正四棱锥S-ABCD中,SA=AB,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点.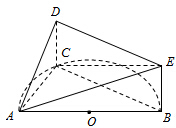 如图,半圆O的直径AB长为4,C是半圆O上除A,B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,sin∠EAB=
如图,半圆O的直径AB长为4,C是半圆O上除A,B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,sin∠EAB=