题目内容
4. 在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,AB=AP=3,AD=PB=2,E为线段AB上一点,且AE:EB=7:2,点F,G,M分别为线段PA、PD、BC的中点.
在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,AB=AP=3,AD=PB=2,E为线段AB上一点,且AE:EB=7:2,点F,G,M分别为线段PA、PD、BC的中点.(1)求证:PE⊥平面ABCD;
(2)若平面EFG与直线CD交于点N,求二面角P-MN-A的余弦值.
分析 (1)推导出PE⊥AB,由此能证明PE⊥平面ABCD.…(4分)
(2)以E为坐标原点,EP、EB、EN分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出二面角P-MN-A的余弦值.
解答 证明:(1)在等腰△APB中,$cos∠ABP=\frac{{\frac{1}{2}PB}}{AB}=\frac{1}{3}$,
则由余弦定理可得$P{E^2}={(\frac{2}{3})^2}+{2^2}-2×\frac{2}{3}×2×\frac{1}{3}=\frac{32}{9}$,∴$PE=\frac{{4\sqrt{2}}}{3}$.…(2分)
∴PE2+BE2=4=PB2,∴PE⊥AB.…(3分)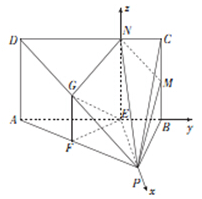
∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
∴PE⊥平面ABCD.…(4分)
解:(2)由已知可得EN∥AD,…(5分)
以E为坐标原点,EP、EB、EN分别为x轴,y轴,z轴,建立空间直角坐标系如图所示,
则$P(\frac{{4\sqrt{2}}}{3},0,0),M(0,\frac{2}{3},1),N(0,0,2)$,
从而$\overrightarrow{PM}=(-\frac{{4\sqrt{2}}}{3},\frac{2}{3},1)$,$\overrightarrow{MN}=(0,-\frac{2}{3},1)$.…(7分)
设平面PMN的法向量为$\vec n=(x,y,z)$,则$\vec n•\overrightarrow{PM}=0$,$\vec n•\overrightarrow{MN}=0$,
即$-\frac{{4\sqrt{2}}}{3}x+\frac{2}{3}y+z=0$,$-\frac{2}{3}y+z=0$,
令y=3,可得平面PMN的一个法向量为$\vec n=(\frac{3}{{\sqrt{2}}},3,2)$.…(9分)
由(1)知平面AMN的一个法向量为$\overrightarrow{EP}=(\frac{{4\sqrt{2}}}{3},0,0)$,…(10分)
$cos\left?{\vec n,\overrightarrow{EP}}\right>=\frac{4}{{\frac{{4\sqrt{2}}}{3}×\frac{{\sqrt{35}}}{{\sqrt{2}}}}}=\frac{{3\sqrt{35}}}{35}$,…(11分)
由图可知二面角P-MN-A的平面角为锐角,
故二面角P-MN-A的余弦值为$\frac{{3\sqrt{35}}}{35}$.…(12分)
点评 本题考查线面垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案| A. | (-∞,-1) | B. | (0,1) | C. | (1,2) | D. | (-1,+∞) |
| X | 0 | 1 | 2 | 3 |
| P | 0.1 | a | b | 0.1 |
| A. | 4 | B. | 7 | C. | 8 | D. | 16 |
| A. | ∅ | B. | [2,4) | C. | [2,+∞) | D. | (4,+∞) |
| A. | (2,3] | B. | [3,4) | C. | (4,5] | D. | [5,6) |
| A. | m1=-1,m2=1 | B. | m=1 | C. | m=-1 | D. | 无解 |
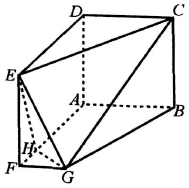 在多面体ABCDEFG中,四边形ABCD与ADEF是边长均为a的正方形,四边形ABGH是直角梯形,AB⊥AF,且FA=2FG=4FH.
在多面体ABCDEFG中,四边形ABCD与ADEF是边长均为a的正方形,四边形ABGH是直角梯形,AB⊥AF,且FA=2FG=4FH.