题目内容
BC是Rt△ABC的斜边,AP⊥平面ABC,PD⊥BC于点D,则图中共有直角三角形的个数是( )
| A.8 | B.7 | C.6 | D.5 |
A
解析试题分析:因为AP⊥平面ABC,BC?平面ABC,所以PA⊥BC,
又PD⊥BC于D,连接AD,PD∩PA=A,所以BC⊥平面PAD,又AD?平面PAD,所以BC⊥AD;
又BC是Rt△ABC的斜边,所以∠BAC为直角,所以图中的直角三角形有:△ABC,△PAC,△PAB,△PAD,△PDC,△PDB,△ADC,△ADB.故答案为:8。
考点:线面垂直的性质定理;线面垂直的判定定理。
点评:本题着重考查了线面垂直性质与判定定理的应用,考查细心分析问题能力,解决问题的能力,属于中档题。

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
设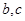 表示两条直线,
表示两条直线,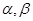 表示两个平面,则下列命题是真命题的是( )
表示两个平面,则下列命题是真命题的是( )
A.若 , ,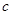 ∥ ∥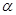 ,则 ,则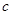 ∥ ∥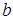 | B.若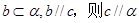 |
C.若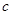 ∥ ∥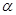 , ,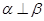 ,则 ,则 | D.若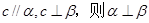 |
如图在棱长均为2的正四棱锥 中,点
中,点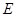 为
为 的中点,则下列命题正确的是( )
的中点,则下列命题正确的是( )
A. 平行面 平行面 ,且直线 ,且直线 到面 到面 距离为 距离为 |
B. 平行面 平行面 ,且直线 ,且直线 到面 到面 距离为 距离为 |
C. 不平行面 不平行面 ,且 ,且 与平面 与平面 所成角大于 所成角大于 |
D. 不平行面 不平行面 ,且 ,且 与面 与面 所成角小于 所成角小于 |
设 、
、 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 |
B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 |
D.若 , , ,则 ,则 |
设 是平面
是平面 内的两条不同直线,
内的两条不同直线, 是平面
是平面 内两条相交直线,则
内两条相交直线,则 的一个充分不必要条件是( )
的一个充分不必要条件是( )
A. | B. |
C. | D. |
如图长方体中,AB=AD=2 ,CC1=
,CC1= ,则二面角C1—BD—C
,则二面角C1—BD—C
的大小为( )
| A.300 | B.450 | C.600 | D.900 |
设 是不同的直线,
是不同的直线, 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
① ②
② ③
③ ④
④
其中正确的个数( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知 和
和 是两条不同的直线,
是两条不同的直线, 和
和 是两个不重合的平面,那么下面给出的条件中一定能推出
是两个不重合的平面,那么下面给出的条件中一定能推出
 的是( )
的是( )
A. ,且 ,且 | B. ∥ ∥ ,且 ,且  |
C. ,且 ,且 ∥ ∥ | D.  ,且 ,且 ∥ ∥ |
 的侧棱长与底面边长都相等,
的侧棱长与底面边长都相等, 是
是 的中点,则
的中点,则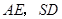 所成的角的余弦值为( )
所成的角的余弦值为( )