题目内容
如图长方体中,AB=AD=2 ,CC1=
,CC1= ,则二面角C1—BD—C
,则二面角C1—BD—C
的大小为( )
| A.300 | B.450 | C.600 | D.900 |
A
解析试题分析:取BD的中点E,连接C1E,CE,因为AB=AD=2 ,所以AC⊥BD,根据三垂线定理可知C1E⊥BD,所以∠C1EC为二面角C1-BD-C的平面角,所以CE=
,所以AC⊥BD,根据三垂线定理可知C1E⊥BD,所以∠C1EC为二面角C1-BD-C的平面角,所以CE= ,而CC1=
,而CC1= ,所以tan∠C1EC=
,所以tan∠C1EC= ,所以二面角C1-BD-C的大小为30°,故答案为:30°。
,所以二面角C1-BD-C的大小为30°,故答案为:30°。
考点:长方体的结构特征;二面角的求法。
点评:本题主要考查了二面角的平面角及求法,考查空间想象能力,逻辑思维能力,计算能力,是中档题.

练习册系列答案
相关题目
设a,b为两条直线, 为两个平面,则下列结论成立的是( )
为两个平面,则下列结论成立的是( )
A.若 且 且 ,则 ,则 | B.若 且 且 ,则 ,则 |
C.若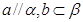 则 则 | D.若 , , ,则 ,则 |
BC是Rt△ABC的斜边,AP⊥平面ABC,PD⊥BC于点D,则图中共有直角三角形的个数是( )
| A.8 | B.7 | C.6 | D.5 |
设 是直线,
是直线, ,
, 是两个不同的平面,下列选项正确的是( )
是两个不同的平面,下列选项正确的是( )
A.若 ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥ | B.若 ∥ ∥ , , ⊥ ⊥ ,则 ,则 ⊥ ⊥ |
C.若 ⊥ ⊥ , , ⊥ ⊥ ,则 ,则 ⊥ ⊥ | D.若 ⊥ ⊥ , ,  ∥ ∥ ,则 ,则 ⊥ ⊥ |
设 是空间三条直线,
是空间三条直线, 是空间两个平面,则下列命题中,逆命题不正确的是( )
是空间两个平面,则下列命题中,逆命题不正确的是( )
A.当 时,若 时,若 ,则 ,则 |
B.当 时,若 时,若 ,则 ,则 |
C.当 且 且 是 是 在 在 内的射影时,若 内的射影时,若 ,则 ,则 |
D.当 且 且 时,若 时,若 ,则 ,则 |
设 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面.考查下列命题,其中正确的命题是( )
是两个不同的平面.考查下列命题,其中正确的命题是( )
A. | B. |
C. | D. |




 在正方体
在正方体 的对角线
的对角线 上.过点
上.过点 的直线,与正方体表面相交于
的直线,与正方体表面相交于 设
设 则函数
则函数 的图象大致是( )
的图象大致是( )