题目内容
如图在棱长均为2的正四棱锥 中,点
中,点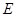 为
为 的中点,则下列命题正确的是( )
的中点,则下列命题正确的是( )
A. 平行面 平行面 ,且直线 ,且直线 到面 到面 距离为 距离为 |
B. 平行面 平行面 ,且直线 ,且直线 到面 到面 距离为 距离为 |
C. 不平行面 不平行面 ,且 ,且 与平面 与平面 所成角大于 所成角大于 |
D. 不平行面 不平行面 ,且 ,且 与面 与面 所成角小于 所成角小于 |
D
解析试题分析:以正方形中心为原点,建立空间坐标系是x轴平行于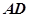 ,y轴平行于
,y轴平行于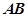 ,z轴为
,z轴为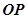 ,所以
,所以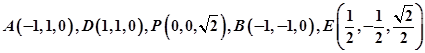 ,直线
,直线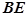 的方向向量为
的方向向量为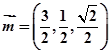 ,平面
,平面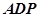 的法向量为
的法向量为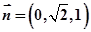 ,所以直线
,所以直线 与面
与面 所成角
所成角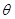 满足
满足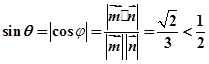
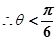
考点:空间线面位置关系及线面所成角
点评:空间向量法求线面角关键是建立合适的坐标系,找准点的坐标,而后代入相应公式计算,本题中线面角公式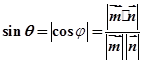

练习册系列答案
相关题目
设m、n表示不同直线, 、
、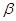 表示不同平面,下列命题正确的是 ( )
表示不同平面,下列命题正确的是 ( )
A.若m‖ ,m‖ n,则n‖ ,m‖ n,则n‖ |
B.若m  ,n ,n  ,m‖ ,m‖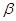 ,n‖ ,n‖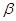 ,则 ,则 ‖ ‖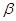 |
C.若  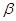 , m , m  ,m ,m n,则n‖ n,则n‖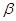 |
D.若  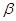 , m , m  ,n‖m,n ,n‖m,n 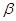 ,则n‖ ,则n‖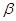 |
如图, 空间四边形ABCD中,若 ,
,
则 与
与 所成角为
所成角为
A. | B. | C. | D. |
如图,长方体ABCD-A1B1C1D1中,AB=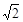 ,BC=CC1=1,则异面直线AC1与BB1所成的角的大小为( )
,BC=CC1=1,则异面直线AC1与BB1所成的角的大小为( )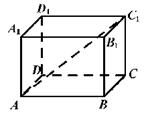
| A.30° | B.45° | C.60° | D.90° |
设a,b为两条直线, 为两个平面,则下列结论成立的是( )
为两个平面,则下列结论成立的是( )
A.若 且 且 ,则 ,则 | B.若 且 且 ,则 ,则 |
C.若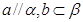 则 则 | D.若 , , ,则 ,则 |
BC是Rt△ABC的斜边,AP⊥平面ABC,PD⊥BC于点D,则图中共有直角三角形的个数是( )
| A.8 | B.7 | C.6 | D.5 |
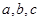 是三条不同的直线,
是三条不同的直线,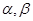 是两个不同的平面,在下列命题:
是两个不同的平面,在下列命题: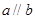 ,且
,且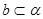 ,则
,则
 ,且
,且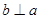 ,则
,则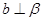
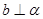 ,则
,则


