题目内容
4.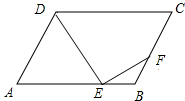 如图,在平行四边形ABCD中,AB=4,AD=2,∠BAD=60°,E,F分别为AB,BC上的点,且AE=2EB,CF=2FB.
如图,在平行四边形ABCD中,AB=4,AD=2,∠BAD=60°,E,F分别为AB,BC上的点,且AE=2EB,CF=2FB.(1)若$\overrightarrow{DE}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,求x,y的值;
(2)求$\overrightarrow{AB$•$\overrightarrow{DE}$的值;
(3)求cos∠BEF.
分析 (1)利用向量的比例关系,即可求出x,y的值.
(2)利用(1)的结果,通过数量积的运算,求解即可.
(3)求出$\overrightarrow{EF}$,通过向量的数量积的运算法则求解cos∠BEF即可.
解答 解:(1)∴$\overrightarrow{DE}=\overrightarrow{AE}-\overrightarrow{AD}=\frac{2}{3}\overrightarrow{AB}-\overrightarrow{AD}$,
∴$x=\frac{2}{3},y=-1$…4
(2)$\overrightarrow{AB}•\overrightarrow{DE}$=$\overrightarrow{AB}•(\frac{2}{3}\overrightarrow{AB}-\overrightarrow{AD})=\frac{2}{3}{\overrightarrow{AB}^2}-\overrightarrow{AB}•\overrightarrow{AD}$…6
=$\frac{2}{3}×{4^2}-4×2×\frac{1}{2}=\frac{20}{3}$…10
(3)设$\overrightarrow{EB},\overrightarrow{EF}$的夹角为θ,
∵$|\overrightarrow{EF}{|^2}=|\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AD}){|^2}=\frac{28}{9}$,
∴$|\overrightarrow{EF}|=\frac{{2\sqrt{7}}}{3}$…12
又∵$\overrightarrow{EF}•\overrightarrow{EB}={\overrightarrow{EB}^2}+\overrightarrow{BF}•\overrightarrow{EB}=\frac{16}{9}+\frac{4}{9}=\frac{20}{9}$,$|\overrightarrow{EB}|=\frac{4}{3}$…14
∴$cosθ=\frac{{\overrightarrow{EB}•\overrightarrow{EF}}}{{|\overrightarrow{EF|}|\overrightarrow{DE}|}}=\frac{{\frac{20}{9}}}{{\frac{{2\sqrt{7}}}{3}×\frac{4}{3}}}=\frac{{5\sqrt{7}}}{14}$…16
点评 本题考查向量的数量积,向量共线的应用,考查转化思想以及计算能力.

| A. | 0和-4 | B. | 0;b取任意实数 | C. | 0和4 | D. | 4;b取任意实数 |
| A. | 2 | B. | -2 | C. | -16 | D. | 16 |
| A. | $\frac{4}{5}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
| A. | 10+2$\sqrt{10}$ | B. | 10+$\sqrt{10}$ | C. | 10-2$\sqrt{10}$ | D. | 10-$\sqrt{10}$ |