题目内容
1.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是( )(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸;③台体的体积公式V=$\frac{1}{3}({S_上}+\sqrt{{S_上}{S_下}}+{S_下})•h$)
| A. | 2寸 | B. | 3寸 | C. | 4寸 | D. | 5寸 |
分析 由题意求得盆中水的上地面半径,代入圆台体积公式求得水的体积,除以盆口面积得答案.
解答 解:如图,由题意可知,天池盆上底面半径为14寸,下底面半径为6寸,高为18寸.
∵积水深9寸,
∴水面半径为$\frac{1}{2}$(14+6)=10寸,
则盆中水的体积为$\frac{1}{3}$π×9(62+102+6×10)=588π(立方寸).
∴平地降雨量等于$\frac{588π}{π×1{4}^{2}}$=3(寸).
故选:B.
点评 本题考查柱、锥、台体的体积求法,正确理解题意是关键,属基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
6.若实数x,y满足不等式$\left\{\begin{array}{l}{2x+y+2≥0}\\{x+y-1≤0}\\{y≥m}\end{array}\right.$,且x-y的最大值为5,则实数m的值为( )
| A. | 0 | B. | -1 | C. | -2 | D. | -5 |
10.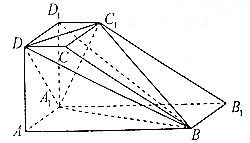 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
(Ⅰ)证明:BD1⊥平面A1C1D;
(Ⅱ)求多面体BDC1A1D1的体积.
 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.(Ⅰ)证明:BD1⊥平面A1C1D;
(Ⅱ)求多面体BDC1A1D1的体积.
11.已知F1、F2为双曲线的焦点,过F2垂直于实轴的直线交双曲线于A、B两点,BF1交y轴于点C,若AC⊥BF1,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
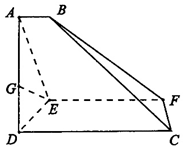 如图,已知梯形CDEF与△ADE所在的平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9,CD=12,连接BC,BF.
如图,已知梯形CDEF与△ADE所在的平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9,CD=12,连接BC,BF.