题目内容
已知{an}是公差为d的等差数列,它的前n项和为Sn,S4=2S2+8.
(Ⅰ)求公差d的值;
(Ⅱ)若a1=1,设Tn是数列{
}的前n项和,求使不等式Tn≥
(m2-5m)对所有的n∈N*恒成立的最大正整数m的值.
(Ⅰ)求公差d的值;
(Ⅱ)若a1=1,设Tn是数列{
| 1 |
| anan+1 |
| 1 |
| 18 |
考点:数列的求和,数列与不等式的综合
专题:综合题,等差数列与等比数列
分析:(Ⅰ)依题意S4=2S2+8,可求得公差d的值;
(Ⅱ)由(Ⅰ)知,d=2,an=2n-1,于是易求
=
(
-
),Tn=
(1-
)≥
,依题意,不等式Tn≥
(m2-5m)对所有的n∈N*恒成立,
解不等式
≥
(m2-5m),即可求得m的最大正整数值.
(Ⅱ)由(Ⅰ)知,d=2,an=2n-1,于是易求
| 1 |
| anan+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 3 |
| 1 |
| 18 |
解不等式
| 1 |
| 3 |
| 1 |
| 18 |
解答:
解:(Ⅰ)∵公差为d的等差数列{an}中,S4=2S2+8,
∴4a1+6d=2(2a1+d)+8,化简得:4d=8,
解得d=2.…(4分)
(Ⅱ)由a1=1,d=2,得an=2n-1,…(5分)
∴
=
=
(
-
).…(6分)
∴Tn=
(1-
+
-
+
-
+…+
-
)
=
(1-
)≥
,…(8分)
又∵不等式Tn≥
(m2-5m)对所有的n∈N*恒成立,
∴
≥
(m2-5m),…(10分)
化简得:m2-5m-6≤0,解得:-1≤m≤6.
∴m的最大正整数值为6.…(12分)
∴4a1+6d=2(2a1+d)+8,化简得:4d=8,
解得d=2.…(4分)
(Ⅱ)由a1=1,d=2,得an=2n-1,…(5分)
∴
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 3 |
又∵不等式Tn≥
| 1 |
| 18 |
∴
| 1 |
| 3 |
| 1 |
| 18 |
化简得:m2-5m-6≤0,解得:-1≤m≤6.
∴m的最大正整数值为6.…(12分)
点评:本题考查数列的求和,考查数列与不等式的综合,考查等价转化思想与恒成立问题,属于难题.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
下列叙述:
①若两条直线平行,则它们的方向向量方向相同或相反;
②若两个向量均为同一个平面的法向量,则以这两个向量为方向向量的直线一定平行;
③若一条直线的方向向量与某一个平面的法向量垂直,则该直线与这个平面平行.
其中正确的个数是( )
①若两条直线平行,则它们的方向向量方向相同或相反;
②若两个向量均为同一个平面的法向量,则以这两个向量为方向向量的直线一定平行;
③若一条直线的方向向量与某一个平面的法向量垂直,则该直线与这个平面平行.
其中正确的个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
下列说法错误的是( )
| A、如果直线上的两点在一个平面内,那么此直线在平面内 |
| B、过空间中三点,有且只有一个平面 |
| C、若两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 |
| D、平行于同一条直线的两条直线互相平行 |
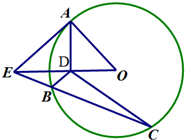 如图,AE是圆O的切线,A是切点,AD⊥OE于D,割线EC交圆O于B、C两点.
如图,AE是圆O的切线,A是切点,AD⊥OE于D,割线EC交圆O于B、C两点.