��Ŀ����
20����֪��M��N��ƽ������$\left\{\begin{array}{l}{2x-y-4��0}\\{x-2y+4��0}\\{x+y-2��0}\end{array}\right.$�ڵ��������㣬$\overrightarrow{a}$=��1��2������$\overrightarrow{MN}$•$\overrightarrow{a}$�����ֵΪ��������| A�� | 2$\sqrt{5}$ | B�� | 10 | C�� | 12 | D�� | 8 |
���� ������������������ƽ�����������������������ļ������弴����$\overrightarrow{a}$�ϵ�ͶӰ�ж�AB�����λ�ã����ɵõ�����
��� 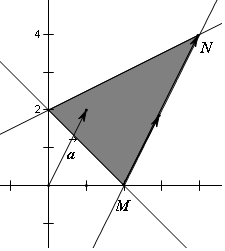 �⣺ƽ������$\left\{\begin{array}{l}{2x-y-4��0}\\{x-2y+4��0}\\{x+y-2��0}\end{array}\right.$�Ŀ�������ͼ��ƽ��$\overrightarrow{a}$���������M��
�⣺ƽ������$\left\{\begin{array}{l}{2x-y-4��0}\\{x-2y+4��0}\\{x+y-2��0}\end{array}\right.$�Ŀ�������ͼ��ƽ��$\overrightarrow{a}$���������M��
�ɿ������֪��$\overrightarrow{MN}•\overrightarrow{a}$�����ֵ����$\overrightarrow{MN}$��$\overrightarrow{a}$�ϵ�ͶӰȡ�����ֵ��
��$\left\{\begin{array}{l}{2x-y-4=0}\\{x+y-2=0}\end{array}\right.$�ɵ�M��2��0������$\left\{\begin{array}{l}{2x-y-4=0}\\{x-2y+4=0}\end{array}\right.$�õ�N��4��4����$\overrightarrow{MN}$=��2��4����
��ʱ$\overrightarrow{MN}$•$\overrightarrow{a}$=1��2+2��4=10��
��ѡ��B��
���� ���⿼�����Թ滮�������������ʾ��ƽ�������������ļ�������Ȼ���֪ʶ���������ν�ϵ���ѧ˼�룬�����е��⣮

��ϰ��ϵ�д�
 ��ѧ��������������Ͼ���ѧ������ϵ�д�
��ѧ��������������Ͼ���ѧ������ϵ�д�
�����Ŀ
8���躯��f��x��=$\left\{\begin{array}{l}{lo{g}_{9}x��x��0}\\{{4}^{-x}+\frac{3}{2}��x��0}\end{array}\right.$����f��27��+f��-log43����ֵΪ��������
| A�� | 6 | B�� | 9 | C�� | 10 | D�� | 12 |
12����֪����z1=a-5i�ڸ�ƽ���϶�Ӧ�ĵ���ֱ��5x+2y=0�ϣ�����z=$\frac{5+2i}{{z}_{1}}$��i��������λ������z2017=��������
| A�� | 1 | B�� | -1 | C�� | -i | D�� | i |
9����-3��a��1���ǡ�����x��R��ʹ��|x-a|+|x+1|��2���ģ�������
| A�� | ��ַDZ�Ҫ���� | B�� | ��Ҫ�dz������ | ||
| C�� | ��Ҫ���� | D�� | �ȷdz���ַDZ�Ҫ���� |
17���������ڣ�-�ޣ�1���ȣ�1��+�ޣ��ϵĺ���y=f��x������f��1+x��=f��1-x�����ҵ�x�ʣ�1��+�ޣ�ʱ��f��x��=|$\frac{2x-3}{x-1}$|�����н����д�����ǣ�������
| A�� | ����t��R��ʹf��x����2��[t-$\frac{1}{2}$��t+$\frac{1}{2}$]�Ϻ���� | |
| B�� | ����t��R��ʹ0��f��x����2��[t-$\frac{1}{2}$��t+$\frac{1}{2}$]�Ϻ���� | |
| C�� | ����t��R��ʹf��x����[t-$\frac{1}{2}$��t+$\frac{1}{2}$]��ʼ�մ��ڷ����� | |
| D�� | ����t��R+��ʹf��x����[t-$\frac{1}{2}$��t+$\frac{1}{2}$]��ʼ�մ��ڷ����� |
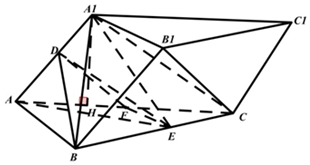 ��ͼ��������ABC-A1B1C1�У�����ACC1A1�͵���ABC����A1AC=60�㣬AC=2AA1=4����D��E�ֱ���AA1��BC���е㣮
��ͼ��������ABC-A1B1C1�У�����ACC1A1�͵���ABC����A1AC=60�㣬AC=2AA1=4����D��E�ֱ���AA1��BC���е㣮