题目内容
17.若定义在(-∞,1)∪(1,+∞)上的函数y=f(x)满足f(1+x)=f(1-x),且当x∈(1,+∞)时,f(x)=|$\frac{2x-3}{x-1}$|则下列结论中错误的是( )| A. | 存在t∈R,使f(x)≥2在[t-$\frac{1}{2}$,t+$\frac{1}{2}$]上恒成立 | |
| B. | 存在t∈R,使0≤f(x)≤2在[t-$\frac{1}{2}$,t+$\frac{1}{2}$]上恒成立 | |
| C. | 存在t∈R,使f(x)在[t-$\frac{1}{2}$,t+$\frac{1}{2}$]上始终存在反函数 | |
| D. | 存在t∈R+,使f(x)在[t-$\frac{1}{2}$,t+$\frac{1}{2}$]上始终存在反函数 |
分析 利用对称性作出f(x)的函数图象,根据图象即可判断出结论.
解答 解:∵f(1+x)=f(1-x),∴f(x)关于直线x=1对称,
作出f(x)的函数图象如图所示: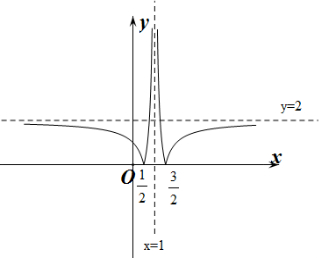
由图象可知f(x)≥2的解集为($\frac{3}{4}$,1)∪(1,$\frac{5}{4}$),
∴不存在一个长度为1的区间[t-$\frac{1}{2}$,t+$\frac{1}{2}$]使得f(x)≥2恒成立,故A错误,
由图象可知0≤f(x)≤2的解集为(-∞,$\frac{3}{4}$)∪($\frac{5}{4}$,+∞),
∴存在一个长度为1的区间[t-$\frac{1}{2}$,t+$\frac{1}{2}$]使得0≤f(x)≤2在[t-$\frac{1}{2}$,t+$\frac{1}{2}$]上恒成立,故B正确;
由图象可知f(x)在(-∞,$\frac{1}{2}$)和($\frac{1}{2}$,+∞)上为单调函数,
∴存在某个区间[t-$\frac{1}{2}$,t$+\frac{1}{2}$]⊆(-∞,$\frac{1}{2}$)∪($\frac{1}{2}$,+∞),使得f(x)在此区间上存在反函数,
故C,D正确;
故选A.
点评 本题考查了函数的对称性判断,函数具有反函数的条件,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.已知点M,N是平面区域$\left\{\begin{array}{l}{2x-y-4≤0}\\{x-2y+4≥0}\\{x+y-2≥0}\end{array}\right.$内的两个动点,$\overrightarrow{a}$=(1,2),则$\overrightarrow{MN}$•$\overrightarrow{a}$的最大值为( )
| A. | 2$\sqrt{5}$ | B. | 10 | C. | 12 | D. | 8 |
9.某学校高三年级有学生500人,其中男生300名,女生200名,为了研究学生的数学成绩(单位:分)是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学成绩,然后按性别分为男、女两组,再将两组学生的数学成绩分成5组,分别加以统计,得到如图所示的频率分布直方图.
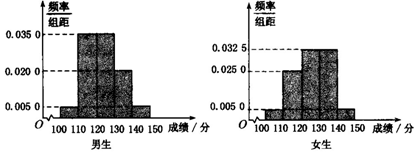
(1)从样本中数学成线小于110分的学生中随机抽取2名学生,求2名学生恰好为一男一女的概率;
(2)若规定数学成绩不小于130分的学生为“数学尖子生”,得到如下数据表:请你根据已知条件完成下列2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
参考数据:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.

(1)从样本中数学成线小于110分的学生中随机抽取2名学生,求2名学生恰好为一男一女的概率;
(2)若规定数学成绩不小于130分的学生为“数学尖子生”,得到如下数据表:请你根据已知条件完成下列2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
| 数学尖子生 | 数学尖子生 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 | 100 |
| P(K2≥k2) | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
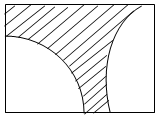 已知矩形的长为10,宽为5(如图所示),在矩形内随机地投掷1000颗黄豆,数得落在阴影部分的黄豆为560颗,则可以估计阴影部分的面积为2.8.
已知矩形的长为10,宽为5(如图所示),在矩形内随机地投掷1000颗黄豆,数得落在阴影部分的黄豆为560颗,则可以估计阴影部分的面积为2.8.