题目内容
11．两条平行直线3x-2y+1=0与6x-4y-2=0之间的距离等于$\frac{{2\sqrt{13}}}{13}$．分析 利用平行线之间的距离公式即可得出．
解答 解：6x-4y-2=0化为：3x-2y-1=0．
∴两条平行直线3x-2y+1=0与6x-4y-2=0之间的距离=$\frac{|-1-1|}{\sqrt{{3}^{2}+（-2）^{2}}}$=$\frac{2\sqrt{13}}{13}$．
故答案为：$\frac{2\sqrt{13}}{13}$．
点评 本题考查了平行线之间的距离公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
1．设x＞0，集合$M=\left\{{{x^2}，{{log}_4}x}\right\}，N=\left\{{{2^x}，a}\right\}$，若M∩N={1}，则M∪N=（ ）
| A． | {0，1，2，4} | B． | {0，1，2} | C． | {1，4} | D． | {0，1，4} |
如图，在多面体ABCDEF中，正三角形BCE所在平面与菱形ABCD所在的平面垂直，FD⊥平面ABCD，且$BC=4，FD=2\sqrt{3}$．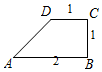
如图，将直角梯形ABCD绕AB边所在的直线旋转一周，由此形成的几何体的体积是$\frac{4π}{3}$．