题目内容
已知二次函数f（x）=x2+bx+c．试说明“b，c均为奇数”是“方程f（x）=0无整数根”的充分而不必要条件．
考点：必要条件、充分条件与充要条件的判断
专题：函数的性质及应用,简易逻辑
分析：根据充分条件和必要条件的对应进行判断即可得到结论．
解答：
证明：充分性：假设方程f（x）=0至少有一个整数根x0．
则
+bx0+c=0．
若x0是奇数，因为b，c均为奇数，所以
+bx0+c为奇数，不可能为0，矛盾；
若x0是偶数，因为b，c均为奇数，所以
+bx0+c为奇数，不可能为0，矛盾．
所以方程f（x）=0无整数根．
所以“b，c均为奇数”是“方程f（x）=0无整数根”的充分条件．
不必要性：令b=1，c=2，方程f（x）=0即x2+x+2=0显然无整数根，但此时c为偶数．
所以“b，c均为奇数”是“方程f（x）=0无整数根”的不必要条件．
综上所述，“b，c均为奇数”是“方程f（x）=0无整数根”的充分而不必要条件．
则
| x | 2 0 |
若x0是奇数，因为b，c均为奇数，所以
| x | 2 0 |
若x0是偶数，因为b，c均为奇数，所以
| x | 2 0 |
所以方程f（x）=0无整数根．
所以“b，c均为奇数”是“方程f（x）=0无整数根”的充分条件．
不必要性：令b=1，c=2，方程f（x）=0即x2+x+2=0显然无整数根，但此时c为偶数．
所以“b，c均为奇数”是“方程f（x）=0无整数根”的不必要条件．
综上所述，“b，c均为奇数”是“方程f（x）=0无整数根”的充分而不必要条件．
点评：本题主要考查充分条件和必要条件的应用，结合二次函数的性质是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
设全集U是实数集R，M={x||2x-3|≥4}，N={x|log
（x+2）≥0}，则M∩N=（ ）
| 1 |
| 3 |
A、{x|x≤-
| ||
B、{x|-2＜x≤-
| ||
C、{x|-
| ||
| D、{x|-2＜x≤-1} |
某产品的广告费用x与销售额y的统计数据如下表：根据上表可得回归方程
=
x+a中的b=10.6，据此模型预报广告费用为10万元时销售额为（ ）
 |
| y |
|
| b |
| 广告费用x（万元） | 4 | 2 | 3 | 5 |
| 销售额y（万元） | 49 | 26 | 39 | 58 |
| A、112.1万元 |
| B、113.1万元 |
| C、111.9万元 |
| D、113.9万元 |
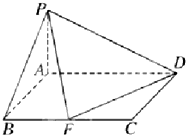已知在四棱锥P-ABCD中，底面ABCD是矩形，且AD=2，AB=1，PA⊥平面ABCD，F为线段BC的中点．