题目内容
18．解方程：（1）x3-7x+6=0
（2）x3-3x2+3x=9．
分析 进行因式分解，然后求解x的值．
解答 解：（1）由x3-7x+6=0，得
x3-x-6x+6=0，
即x（x-1）（x+1）-6（x-1）=0，
即（x-1）（x2+x-6）=0．
即（x-1）（x+3）（x-2）=0
解得：x=-3或x=1或x=2；
（2）x3-3x2+3x=9，得
x3-3x2+3x-9=0，
即x2（x-3）+3（x-3）=0，
即（x-3）（x2+3）=0，
解得x=3．
点评 本题考查了一元三次方程的解法，关键是正确进行因式分解，是基础题．
练习册系列答案
相关题目
8．已知（1+x）20=a0+a1x+a2x2+…+a20x20，则$\frac{{a}_{1}+2{a}_{2}+3{a}_{3}+…+10{a}_{10}}{{2}^{10}}$的值为（ ）
| A． | 20 | B． | 15 | C． | 5 | D． | 1 |
13．设i为虚数单位，复数$\frac{1+i}{2+bi}$为纯虚数，则实数b等于（ ）
| A． | 2 | B． | 1 | C． | -1 | D． | -2 |
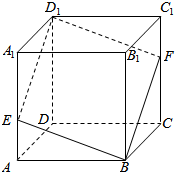已知E，F分别是正方体A1B1C1D1-ABCD的棱AA1，CC1上的点，且A1E=2EA，CF=2FC1，求证：四边形BED1F是平行四边形．