题目内容
13.设i为虚数单位,复数$\frac{1+i}{2+bi}$为纯虚数,则实数b等于( )| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
分析 化简可得已知复数,由纯虚数的定义可得.
解答 解:化简可得$\frac{1+i}{2+bi}=\frac{(1+i)(2-bi)}{(2+bi)(2-bi)}=\frac{(2+b)+(2-b)i}{{4+{b^2}}}$,
由纯虚数定义可得2+b=0且2-b≠0,解得b=-2.
故选:D
点评 本题考查复数的代数形式的运算,涉及复数的基本概念,属基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
4.函数y=ln(x2)+x3的图象大致是( )
| A. | 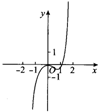 | B. | 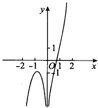 | C. | 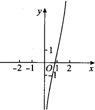 | D. | 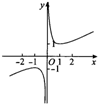 |
2.过点M(3,2)的抛物线方程是( )
| A. | x2=$\frac{9}{2}$y | B. | y2=$\frac{4}{3}$x | C. | y2=$\frac{4}{3}$x或 x2=$\frac{9}{2}$y | D. | y2=$\frac{3}{4}$x或x2=$\frac{2}{9}$y |