题目内容
7．
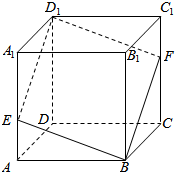已知E，F分别是正方体A1B1C1D1-ABCD的棱AA1，CC1上的点，且A1E=2EA，CF=2FC1，求证：四边形BED1F是平行四边形．
分析 可在该正方体的棱BB1上取点G，使得BG=2GB1，这样容易说明四边形A1EBG为平行四边形，从而有BE∥A1G，且BE=A1G，同理可说明四边形GFCB为平行四边形．从而可得到GF∥BC，且GF=BC，这样便可得到四边形GFD1A1为平行四边形，从而得出A1G∥D1F，且A1G=D1F，这样便可得出四边形BED1F为平行四边形．
解答 证明：如图，在棱BB1上取点G，使BG=2GB1，连接A1G，FG；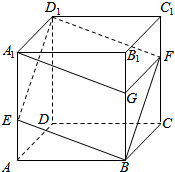
A1E=2EA；
∴A1E∥BG，且A1E=BG；
∴四边形A1EBG为平行四边形；
∴BE∥A1G，且BE=A1G；
同理，GF∥BC，GF=BC；
又BC∥A1D1，且BC=A1D1；
∴GF∥A1D1，且GF=A1D1；
∴四边形GFD1A1为平行四边形；
∴A1G∥D1F，且A1G=D1F；
∴BE∥D1F，且BE=D1F；
∴四边形BED1F为平行四边形．
点评 考查平行四边形的定义，根据一组对边平行且相等来判定一个四边形为平行四边形的方法．
练习册系列答案
相关题目
15．若x∈（0，$\frac{π}{2}$），$y∈（0，\frac{π}{2}）$，且tan2x=3tan（x-y），则x+y的可能取值是（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{7π}{12}$ |
2．过点M（3，2）的抛物线方程是（ ）
| A． | x2=$\frac{9}{2}$y | B． | y2=$\frac{4}{3}$x | C． | y2=$\frac{4}{3}$x或 x2=$\frac{9}{2}$y | D． | y2=$\frac{3}{4}$x或x2=$\frac{2}{9}$y |