题目内容
已知函数f(x)=2x3-3x.
(1)求f(x)在区间[-2,1]上的最大值;
(2)若过点P(1,t)存在3条直线与曲线y=f(x)相切,求t的取值范围;
(3)问过点A(-1,2),B(2,10),C(0,2)分别存在几条直线与曲线y=f(x)相切?(只需写出结论)
解 (1)由f(x)=2x3-3x得f′(x)=6x2-3.
令f′(x)=0,得x=-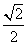 或x=
或x=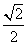 .
.
因为f(-2)=-10,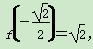 ,
,
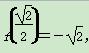 ,f(1)=-1.
,f(1)=-1.
所以f(x)在区间[-2,1]上的最大值为
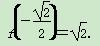 (2)设过点P(1,t)的直线与曲线y=f(x)相切于点(x0,y0).
(2)设过点P(1,t)的直线与曲线y=f(x)相切于点(x0,y0).
则y0=2x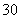 -3x0,且切线斜率为k=6x
-3x0,且切线斜率为k=6x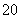 -3,
-3,
所以切线方程为y-y0=(6x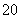 -3)(x-x0).
-3)(x-x0).
因此t-y0=(6x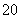 -3)(1-x0).
-3)(1-x0).
整理得4x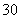 -6x
-6x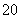 +t+3=0.
+t+3=0.
设g(x)=4x3-6x2+t+3,
则“过点P(1,t)存在3条直线与曲线y=f(x)相切”等价于“g(x)有3个不同零点”.
g′(x)=12x2-12x=12x(x-1),
g(x)与g′(x)的情况如下:
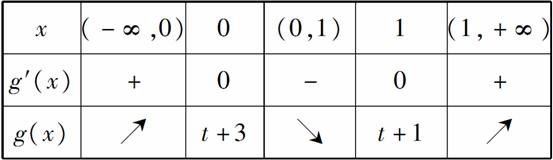
所以g(0)=t+3是g(x)的极大值,g(1)=t+1是g(x)的极小值.
当g(0)=t+3≤0,即t≤-3时,此时g(x)在区间(-∞,1]和(1,+∞)上分别至多有1个零点,所以g(x)至多有2个零点.
当g(1)=t+1≥0,即t≥-1时,此时g(x)在区间(-∞,0)和[0,+∞)上分别至多有1个零点,所以g(x)至多有2个零点.
当g(0)>0且g(1)<0,即-3<t<-1时,因为g(-1)=t-7<0,g(2)=t+11>0,所以g(x)分别在区间[-1,0),[0,1)和[1,2)上恰有1个零点,由于g(x)在区间(-∞,0)和(1,+∞)上单调,所以g(x)分别在区间(-∞,0)和[1,+∞)上恰有1个零点.
综上可知,当过点P(1,t)存在3条直线与曲线y=f(x)相切时,t的取值范围是(-3,-1).
(3)过点A(-1,2)存在3条直线与曲线y=f(x)相切;
过点B(2,10)存在2条直线与曲线y=f(x)相切;
过点C(0,2)存在1条直线与曲线y=f(x)相切.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案 (x2-4)的单调递增区间为( )
(x2-4)的单调递增区间为( ) ,e<a<b,则( )
,e<a<b,则( )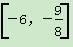
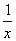 的导函数,则下列结论中正确的是( )
的导函数,则下列结论中正确的是( ) +
+  的定义域是________.
的定义域是________.