题目内容
已知函数f(x)＝x3－3x及y＝f(x)上一点P(1，－2)，过点P作直线l.
(1)求使直线l和y＝f(x)相切且以P为切点的直线方程；
(2)求使直线l和y＝f(x)相切且切点异于P的直线方程．
解 (1)由f(x)＝x3－3x得f′(x)＝3x2－3，
过点P且以P(1，－2)为切点的直线的斜率f′(1)＝0，
∴所求的直线方程为y＝－2.
(2)设过P(1，－2)的直线l与y＝f(x)切于另一点(x0，y0)，
则f′(x0)＝3x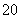
－3.
又直线过(x0，y0)，P(1，－2)．
故其斜率可表示为
又
即x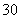
－3x0＋2＝3(x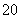－1)(x0－1)，
解得x0＝1(舍去)或x0＝－
，
故所求直线的斜率为k＝3×
＝－
.
∴y－(－2)＝－(x－1)，即9x＋4y－1＝0.
练习册系列答案
相关题目
，函数g(x)＝
则函数g(x)的最小值是________．
＋
.
，使f(x0)＝x0.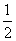
n(n＋1)(2n＋1)吨，但如果年产量超过150吨，会给环境造成危害，为保护环境，环保部门应给该厂这条生产线拟定最长的生产期限是( )