题目内容
已知函数f(x)=log4(4x+1)+kx(k∈R)为偶函数.
(1)求k的值;
(2)若方程f(x)=log4(a·2x-a)有且只有一个根,求实数a的取值范围.
解 (1)∵f(x)为偶函数,∴f(-x)=f(x),
即log4(4-x+1)-kx=log4(4x+1)+kx,
即(2k+1)x=0,∴k=-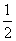 .
.
(2)依题意有log4(4x+1)-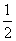 x=log4(a·2x-a),
x=log4(a·2x-a),
即
令t=2x,则(1-a)t2+at+1=0(*),
只需其有一正根即可满足题意.
①当a=1,t=-1时,不合题意.
②(*)式有一正一负根t1,t2,
即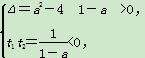
得a>1,经验证正根满足at-a>0,∴a>1.
③(*)式有相等两根,即Δ=0⇒a=±2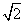 -2,
-2,
此时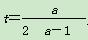 ,
,
若a=2(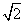 -1),则有
-1),则有 ,此时方程(1-a)t2+at+1=0无正根,故a=2(
,此时方程(1-a)t2+at+1=0无正根,故a=2(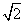 -1)舍去;
-1)舍去;
 因此a=-2(
因此a=-2(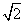 +1).
+1).
综上所述,a>1或a=-2-2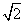 .
.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目

 +
+ .
. ,使f(x0)=x0.
,使f(x0)=x0.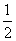 n(n+1)(2n+1)吨,但如果年产量超过150吨,会给环境造成危害,为保护环境,环保部门应给该厂这条生产线拟定最长的生产期限是( )
n(n+1)(2n+1)吨,但如果年产量超过150吨,会给环境造成危害,为保护环境,环保部门应给该厂这条生产线拟定最长的生产期限是( )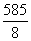 -u与
-u与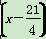 2成正比,且售价为10元时,年销量为28万件.
2成正比,且售价为10元时,年销量为28万件.