题目内容
9.已知数列{an}的前n项和Sn满足Sn+an=2n+1,(1)写出a1,a2,a3并猜想an的表达式;
(2)用数学归纳法证明(1)中的猜想.
分析 (1)利用Sn+an=2n+1,代入计算,可得结论,猜想an=2-$\frac{1}{{2}^{n}}$(n∈N*).
(2)用归纳法进行证明,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
解答 解:(1)由Sn+an=2n+1得a1=$\frac{3}{2}$,a2=$\frac{7}{4}$,a3=$\frac{15}{8}$,
故猜想an=$\frac{{2}^{n+1}-1}{{2}^{n}}$=2-$\frac{1}{{2}^{n}}$(n∈N*).
(2)证明①当n=1时a1=$\frac{3}{2}$,结论成立,
②假设当n=k时结论成立,即ak=2-$\frac{1}{{2}^{k}}$,
则当n=k+1时,ak+1=Sk+1-Sk=2(k+1)+1-ak+1-(2k+1-a(2k+1-ak))
∴2ak+1=ak+2=4-$\frac{1}{{2}^{k}}$,∴ak+1=2-$\frac{1}{{2}^{k+1}}$,即当n=k+1时结论成立.
由①②知对于任何正整数n,结论成立.
点评 此题主要考查归纳法的证明,归纳法一般三个步骤:(1)验证n=1成立;(2)假设n=k成立;(3)利用已知条件证明n=k+1也成立,从而得证,这是数列的通项一种常用求解的方法

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
17.设f(x)=$f(x)=\left\{\begin{array}{l}{x+2(x≤-1)}\\{{x}^{2}(-1<x<2)}\\{2x(x≥2)}\end{array}\right.$.若f(x)=3.则x的值为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | $\frac{3}{2}$ |
14.已知sin($\frac{π}{3}$+a)=$\frac{5}{13}$,且a∈($\frac{π}{6}$,$\frac{2π}{3}$),则sin($\frac{π}{12}$+a)的值是( )
| A. | $\frac{17\sqrt{2}}{26}$ | B. | $\frac{-7\sqrt{2}}{26}$ | C. | -$\frac{17\sqrt{2}}{26}$ | D. | $\frac{7\sqrt{2}}{26}$ |
1.已知集合A={x|y=ln(x-a)},B={-2,2,3},A∩B=B,则实数a的取值范围是( )
| A. | (-2,+∞) | B. | (3,+∞) | C. | (-∞,-2) | D. | (-∞,3) |
7.经过3小时35分钟,时针与分针转过的度数之差是( )
| A. | 1182.5° | B. | -1182.5° | C. | 1182.3° | D. | -1182.3° |
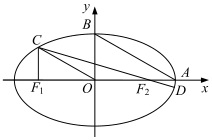 如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.