题目内容
4.已知函数f(x)的导函数为f′(x),且函数f(x)=x2+ax•f′(1)的图象在点(1,f(1))处的切线斜率为-2,则a=2.分析 求出f(x)的导数,再令x=1,可得切线的斜率,由已知条件,可得a的方程,解方程可得a的值.
解答 解:函数f(x)=x2+ax•f′(1)
导数为f′(x)=2x+af′(1),
可得f′(1)=2+af′(1),
由图象在点(1,f(1))处的切线斜率为-2,
可得f′(1)=-2,
即有-2=2-2a,
解得a=2.
故答案为:2.
点评 本题考查导数的运用:求切线的斜率,考查导数的几何意义,考查化简整理的运算能力,属于基础题.

练习册系列答案
相关题目
19.函数f(x)=loga(x+1)(a>0且a≠1)的图象恒过定点( )
| A. | (1,1) | B. | (0,0) | C. | (0,1) | D. | (1,0) |
13.在平面直角坐标系xOy中,设A,B,C是圆x2+y2=1上相异三点,若存在正实数λ,? 使得 $\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,则λ2+(?-3)2的取值范围是( )
| A. | [0,+∞) | B. | (2,+∞) | C. | (2,8) | D. | (8,+∞) |
2.如图,∠ACB=90°,CD⊥AB于D,AD=3,CD=2,则$\frac{AC}{BC}$的值为( )
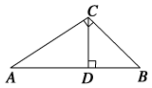

| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{9}$ |