题目内容
已知等比数列{an}，a2•a5•a8=
，则数列{log2an}的前9项和等于（ ）
| 1 |
| 8 |
| A、-9 | B、-8 | C、-7 | D、-10 |
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：利用等比数列的性质，求出a5=
，再求出数列{log2an}的前9项和．
| 1 |
| 2 |
解答：
解：∵数列{an}是等比数列，
∴a2•a8=a52，
又a2•a5•a8=
，
∴a5=
．
∴数列{log2an}的前9项和等于log2a1•a2•…•a9=log2a59=-9．
故选：A．
∴a2•a8=a52，
又a2•a5•a8=
| 1 |
| 8 |
∴a5=
| 1 |
| 2 |
∴数列{log2an}的前9项和等于log2a1•a2•…•a9=log2a59=-9．
故选：A．
点评：本题考查了等比数列的性质与前n项和，考查对数运算，是基础题．
练习册系列答案
相关题目
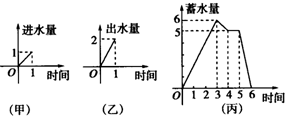水池有两个相同的进水口和一个出水口，每个口进出水速度如下图（甲）、（乙）所示，某天0点到6点该水池蓄水量如图（丙）所以（至少打开一个水口）给出以下3个论断：已知函数f（x）=|x-1|，则下列函数与f（x）相等的函数是（ ）
A、g（x）=
| |||||||
B、g（x）=
| |||||||
C、g（x）=
| |||||||
| D、g（x）=x-1 |