题目内容
12.设数列{an}满足${a_1}=1,{a_{n+1}}=2{a_n}+1,({n∈{N^*}})$,则{an}的通项公式是( )| A. | 2n-1 | B. | 2n | C. | 2n+1 | D. | 2n-1 |
分析 由已知数列递推式可得数列{an+1}是以2为首项,以2为公比的等比数列,求出其通项公式后可得{an}的通项公式.
解答 解:由an+1=2an+1,得an+1+1=2(an+1),
∵a1+1=2≠0,
∴$\frac{{a}_{n+1}+1}{{a}_{n}+1}=2$,
则数列{an+1}是以2为首项,以2为公比的等比数列,
则${a}_{n}+1={2}^{n}$,
∴${a}_{n}={2}^{n}-1$.
故选:A.
点评 本题考查数列递推式,训练了利用构造法求数列的通项公式,是中档题.

练习册系列答案
相关题目
3.已知tanα=$\frac{1}{3}$,则$\frac{sinα-co{s}^{3}α}{sinα+cosα}$=( )
| A. | -$\frac{17}{40}$ | B. | -$\frac{5}{16}$ | C. | -$\frac{34}{45}$ | D. | -$\frac{1}{2}$ |
7.下列四个图形中,不是以x为自变量的函数的图象是( )
| A. |  | B. |  | C. |  | D. |  |
1.$\frac{{\sqrt{3}-tan{{15}^0}}}{{\sqrt{3}tan{{15}^0}+1}}$=( )
| A. | -1 | B. | $\frac{{\sqrt{3}}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
 已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x(x-2).
已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x(x-2).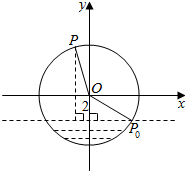 如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.
如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.