题目内容
将一颗质地均匀的正方体骰子(六个面的点数分别为1、2、3、4、5、6)先后抛两次,将得到的点数分别记为a,b.
(1)求满足条件a+b≥9的概率;
(2)求直线ax+by+5=0与x2+y2=1相切的概率
(3)将a,b,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
(1)求满足条件a+b≥9的概率;
(2)求直线ax+by+5=0与x2+y2=1相切的概率
(3)将a,b,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
考点:古典概型及其概率计算公式,直线与圆的位置关系
专题:概率与统计
分析:利用古典概型概率计算公式求解.
解答:
解:(Ⅰ) 先后2次抛掷一枚骰子,将得到的点数分别记为a,b,
事件总数为6×6=36.
满足条件a+b≥9的基本事件有10种:
3+6,4+5,4+6,5+4,5+5,5+6,6+3,6+4,6+5,6+6,…(2分)
∴满足条件a+b≥9的概率是p1=
=
.…(4分)
(Ⅱ)先后2次抛掷一枚骰子,将得到的点数分别记为a,b,
事件总数为6×6=36.
∵直线ax+by+5=0与圆x2+y2=1相切,
∴
=1,即:a2+b2=25,…(6分)
由于a,b∈{1,2,3,4,5,6},∴满足条件的情况只有a=3,b=4或a=4,b=3两种情况.
∴直线ax+by+5=0与圆x2+y2=1相切的概率是p2=
=
.…(8分)
(Ⅲ)先后2次抛掷一枚骰子,将得到的点数分别记为a,b,
事件总数为6×6=36,∵三角形的一边长为5,
当a=1时,b=5,(1,5,5),1种
当a时,b=5,(2,5,5),1种
当a=3时,b=3或5,(2,3,5)(3,5,5),2种,…(11分)
当a=4时,b=4或5,(4,4,5)(4,5,5),2种,
当a=5时,b=1,2,3,4,5,6,(5,1,5)(5,2,5),(5,3,5),(5,4,5),(5,5,5),(5,6,5),6种,
当a=6时,b=5,6,(6,5,5)(6,6,5),2种
故满足条件的不同情况共有14种.
∴三条线段能围成不同的等腰三角形的概率为p3=
=
. …(14分)
事件总数为6×6=36.
满足条件a+b≥9的基本事件有10种:
3+6,4+5,4+6,5+4,5+5,5+6,6+3,6+4,6+5,6+6,…(2分)
∴满足条件a+b≥9的概率是p1=
| 10 |
| 36 |
| 5 |
| 18 |
(Ⅱ)先后2次抛掷一枚骰子,将得到的点数分别记为a,b,
事件总数为6×6=36.
∵直线ax+by+5=0与圆x2+y2=1相切,
∴
| 5 | ||
|
由于a,b∈{1,2,3,4,5,6},∴满足条件的情况只有a=3,b=4或a=4,b=3两种情况.
∴直线ax+by+5=0与圆x2+y2=1相切的概率是p2=
| 2 |
| 36 |
| 1 |
| 18 |
(Ⅲ)先后2次抛掷一枚骰子,将得到的点数分别记为a,b,
事件总数为6×6=36,∵三角形的一边长为5,
当a=1时,b=5,(1,5,5),1种
当a时,b=5,(2,5,5),1种
当a=3时,b=3或5,(2,3,5)(3,5,5),2种,…(11分)
当a=4时,b=4或5,(4,4,5)(4,5,5),2种,
当a=5时,b=1,2,3,4,5,6,(5,1,5)(5,2,5),(5,3,5),(5,4,5),(5,5,5),(5,6,5),6种,
当a=6时,b=5,6,(6,5,5)(6,6,5),2种
故满足条件的不同情况共有14种.
∴三条线段能围成不同的等腰三角形的概率为p3=
| 14 |
| 36 |
| 7 |
| 18 |
点评:本题考查概率的计算,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
设实数x,y满足
则z=
的取值范围是( )
|
| 2x+y+2 |
| x+1 |
A、[
| ||
B、[
| ||
C、[1,
| ||
| D、[1,3] |
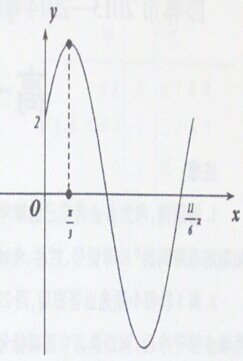 已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<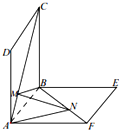 如图正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a< 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.