题目内容
14.在三棱锥P-ABC内任取一点Q,使VQ-ABC<$\frac{1}{3}{V_{P-ABC}}$的概率等于$\frac{19}{27}$.分析 取高线的$\frac{1}{3}$点,过该点作平行于底的平面,若VQ-ABC<$\frac{1}{3}{V_{P-ABC}}$,则Q点在平面DEF与底面ABC之间,所以概率为棱台与原棱锥体积之比,用相似比计算即可.
解答 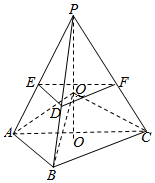 解:作出P在底面△ABC的射影为O
解:作出P在底面△ABC的射影为O
若VQ-ABC=$\frac{1}{3}$VP-ABC,则高OQ=$\frac{1}{3}$PO,
则VQ-ABC<$\frac{1}{3}{V_{P-ABC}}$的点Q位于在三棱锥VP-ABC的截面DEF以下的棱台内,
则对应的概率P=1-($\frac{2}{3}$)3=$\frac{19}{27}$,
故答案为:$\frac{19}{27}$.
点评 本题主要考查几何概型的概率计算,求出对应的体积关系是解决本题的关键,根据比例关系,得到面积之比是相似比的平方,体积之比是相似比的立方.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
4.设抛物线x2=2py(8≥p>0)的焦点为F,点A、B为抛物线上两个动点,过弦AB的中点M作抛物线的准线的垂线MN,垂足为N,当|AF|•|BF|=16时,|MN|的最小值为( )
| A. | 6 | B. | 4 | C. | 8 | D. | 16 |
5.计算机执行下面的程序段后,输出的结果是( )
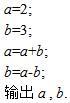
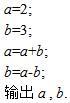
| A. | 5,2 | B. | -1,5 | C. | 5,-1 | D. | 2,5 |
9.已知复数z满足|z|=1,则|z+3-4i|(i为虚数单位)的最大值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
19.sin(-510°)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
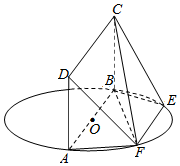 如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在平面和圆O所在的平面互相垂直.已知AB=2,EF=1.
如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在平面和圆O所在的平面互相垂直.已知AB=2,EF=1.