题目内容
函数y=log2x+log2(4-x)的值域为 .
考点:对数函数的值域与最值,对数的运算性质
专题:计算题,函数的性质及应用
分析:由对数的真数大于0可得函数的定义域,将函数解析式化成log2[x(4-x)]后,考虑x(1-x)这个二次函数的值域,即可得出结论.
解答:
解:∵函数f(x)=log2x+log2(4-x)中,x>0且4-x>0,
故f(x)的定义域是(0,4);
∵函数f(x)=log2x+log2(4-x)=log2[x(4-x)]
∵0<x<4,
∴0<x(4-x)≤[
]2=4
∴log2[x(4-x)]≤2,
∴函数y=log2x+log2(4-x)的值域为(-∞,2].
故答案为:(-∞,2]
故f(x)的定义域是(0,4);
∵函数f(x)=log2x+log2(4-x)=log2[x(4-x)]
∵0<x<4,
∴0<x(4-x)≤[
| x+(4-x) |
| 2 |
∴log2[x(4-x)]≤2,
∴函数y=log2x+log2(4-x)的值域为(-∞,2].
故答案为:(-∞,2]
点评:解决对数函数中的最值问题,一是利用对数函数的性质;二是转化为二次函数型,必须充分挖掘问题中的隐含条件进行合理地转化.

练习册系列答案
相关题目
若复数i满足z(1+i)=2i,则在复平面内z对应的点的坐标是( )
| A、(1,1) |
| B、(1,-1) |
| C、(-1,1) |
| D、(-1,-1) |
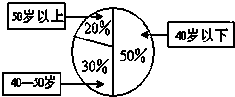 某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号,…,196-200号).若第6组抽出的号码为28,则第8组抽出的号码应是a; 若用分层抽样方法,则50岁以下年龄段应抽取b人.那么a+b等于( )
某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号,…,196-200号).若第6组抽出的号码为28,则第8组抽出的号码应是a; 若用分层抽样方法,则50岁以下年龄段应抽取b人.那么a+b等于( )