题目内容
已知曲线C的方程是y2=4x,设A(x1,y1),B(x2,y2),D(x3,y3)是曲线C上的点,且|
|,|
|,|
|成等差数列,当AD的垂直平分线与x轴交于点E(3,0)时,求B点的坐标.
| AF |
| BF |
| DF |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由抛物线的焦半径公式把|
|,|
|,|
|用三点A、B、D的坐标表示,根据|
|,|
|,|
|成等差数列把B的坐标用A,B的坐标表示,然后写出AD的斜率,AD的中垂线的斜率,由斜率之积等于-1得到B的横坐标的值,代入抛物线方程求得B的坐标.
| AF |
| BF |
| DF |
| AF |
| BF |
| DF |
解答:
由抛物线的定义,知|AF|=x1+1,|BF|=x2+1,|DF|=x3+1,
∵|
|,|
|,|
|成等差数列,
∴2x2+2=x1+1+x3+1,即x2=
.
∵线段AD的中点为(
,
),且线段AD的垂直平分线与x轴交于点E(3,0),
∴线段AD的垂直平分线的斜率为k=
.
又kAD=
,
∴
•
=-1,
即
=-1.
∵x1≠x3,∴x1+x3=2,
又x2=
,
∴x2=1.
∵点B在抛物线上,
∴y22=4x2=4,y2=±2.
∴B(1,2)或(1,-2).
∵|
| AF |
| BF |
| DF |
∴2x2+2=x1+1+x3+1,即x2=
| x1+x3 |
| 2 |
∵线段AD的中点为(
| x1+x3 |
| 2 |
| y1+y3 |
| 2 |
∴线段AD的垂直平分线的斜率为k=
| ||
|
又kAD=
| y3-y1 |
| x3-x1 |
∴
| y3-y1 |
| x3-x1 |
| y1+y3 |
| x1+x3-6 |
即
| 4x3-4x1 |
| (x32-x12)-6(x3-x1) |
∵x1≠x3,∴x1+x3=2,
又x2=
| x1+x3 |
| 2 |
∴x2=1.
∵点B在抛物线上,
∴y22=4x2=4,y2=±2.
∴B(1,2)或(1,-2).
点评:本题考查了抛物线的简单几何性质,考查了抛物线的方程,体现了整体运算思想方法,是中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
圆锥侧面展开图是半径为a的半圆,这个圆锥的高是( )
| A、a | ||||
B、
| ||||
C、
| ||||
D、
|
已知集合P={x|0≤x≤4},集合N={y|0≤y≤2},下列从P到Q的各对应关系f不是函数的是( )
A、f:x→y=
| ||
B、f:x→y=
| ||
C、f:x→y=
| ||
D、f:x→y=
|
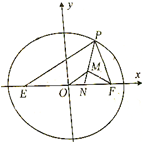 如图,E、F是椭圆G:
如图,E、F是椭圆G:| x2 |
| 4 |
| y2 |
| 3 |
| A、(0,1] | ||||
| B、[-1,1] | ||||
C、[0,
| ||||
| D、[0,1) |
 如图,在四边形ABCD中,AB=CD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连接BE交AC于点F,连接DF.
如图,在四边形ABCD中,AB=CD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连接BE交AC于点F,连接DF. 如图,点P为⊙O的弦AB上的一点,连接OP,过点P作PC⊥OP,PC为⊙O于点C,若OC=4,∠POC=60°,则PA•PB=
如图,点P为⊙O的弦AB上的一点,连接OP,过点P作PC⊥OP,PC为⊙O于点C,若OC=4,∠POC=60°,则PA•PB=