题目内容
13.已知函数f(x)=x•(lnx-2)+$\frac{1}{2}$x2,求f(x)的单调区间.分析 求出函数f(x)的导数,判断出f′(x)的单调性,结合f′(0)=0,求出f′(x)的符号,从而求出函数的单调区间.
解答 解:函数f(x)的定义域是(0,+∞),
f′(x)=(lnx-2)+x(lnx-2)′+x=lnx-1+x,
f″(x)=1+$\frac{1}{x}$>0,
∴f′(x)在(0,+∞)递增,
而f′(1)=0,
∴x∈(0,1)时,f′(x)<0,x∈(1,+∞)时,f′(x)>0,
∴f(x)在(0,1)递减,在(1,+∞)递增.
点评 本题考查了函数的单调性问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
1.已知二次函数y=f(x),当x=2时,函数f(x)取最小值-1,且f(1)+f(4)=3.
(1)求f(x)的解析式;
(2)若g(x)=f(x)-kx在区间(1,4)上无最小值,求实数k的取值范围.
(1)求f(x)的解析式;
(2)若g(x)=f(x)-kx在区间(1,4)上无最小值,求实数k的取值范围.
18.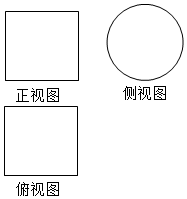 如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )
如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )
 如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )
如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )| A. | 4π | B. | 6π | C. | 8π | D. | 16π |
5.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 16-π | B. | 8+π | C. | 16+π | D. | 8-π |
2.函数f(x)=|lgx|-sinx的零点个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |