题目内容
设0<x<
,若8x≥(2-kx)(4x-3)恒成立,则实数k的最大值为 .
| 3 |
| 4 |
考点:函数恒成立问题
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:先把原不等式整理为k≤
,则问题转化为k≤(
)min,利用基本函数的单调性可求得最小值,从而可得k的范围,于是得到答案.
| -6 |
| 4x2-3x |
| -6 |
| 4x2-3x |
解答:
解:∵0<x<
,
∴8x≥(2-kx)(4x-3)可整理为k≤
,
而4x2-3x=4(x-
)2-
,
由0<x<
,得-
≤4x2-3x<0,
∴
≥
=
,
∴k≤
,即k的最大值为
,
故答案为:
.
| 3 |
| 4 |
∴8x≥(2-kx)(4x-3)可整理为k≤
| -6 |
| 4x2-3x |
而4x2-3x=4(x-
| 3 |
| 8 |
| 9 |
| 16 |
由0<x<
| 3 |
| 4 |
| 9 |
| 16 |
∴
| -6 |
| 4x2-3x |
| -6 | ||
-
|
| 32 |
| 3 |
∴k≤
| 32 |
| 3 |
| 32 |
| 3 |
故答案为:
| 32 |
| 3 |
点评:该题考查函数恒成立、不等式、二次函数的性质等知识,考查学生分析转化能力.

练习册系列答案
相关题目
定义:在数列{an}中,若满足
-
=d(n∈N+,d 为常数),称{an}为“等差比数列”.已知在“等差比数列”{an}中,a1=a2=1,a3=3,则
=( )
| an+2 |
| an+1 |
| an+1 |
| an |
| a2014 |
| a2012 |
| A、4×20122-1 |
| B、4×20132-1 |
| C、4×20142-1 |
| D、4×20132 |
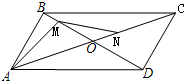 如图,在平行四边形ABCD中,AD=2AB=2,∠BAD=60°,M、N分别是对角线BD、AC上的点,AC、BD相交于点O,已知BM=
如图,在平行四边形ABCD中,AD=2AB=2,∠BAD=60°,M、N分别是对角线BD、AC上的点,AC、BD相交于点O,已知BM=