题目内容
9.求(x$\sqrt{x}$-$\frac{1}{x}$)6的展开式中,含x4项的系数.分析 根据二项式(x$\sqrt{x}$-$\frac{1}{x}$)6展开式的通项公式,即可求出展开式中含x4项的系数.
解答 解:(x$\sqrt{x}$-$\frac{1}{x}$)6展开式的通项公式为:
Tr+1=${C}_{6}^{r}$•${(x\sqrt{x})}^{6-r}$•${(-\frac{1}{x})}^{r}$=(-1)r•${C}_{6}^{r}$•${x}^{9-\frac{5}{2}r}$,
令9-$\frac{5}{2}$r=4,解得r=2;
所以第r+1项的系数为(-1)2•${C}_{6}^{2}$=15,
即含x4项的系数为15.
点评 本题主要考查二项式定理的应用以及利用二项式展开式的通项公式求展开式中某项的系数的应用问题,是中档题

练习册系列答案
相关题目
19.已知集合M满足{1,2}⊆M?{1,2,3,4},则集合M的个数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
20.函数y=x+$\frac{1}{x-1}$+1(x>1)的最小值是( )
| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
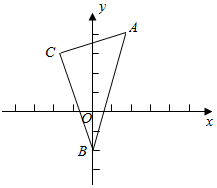 如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求:
如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求: