题目内容
10. 如图,在正方体ABCD-A1B1C1D1中,M为BB1的中点,则直线MC与平面ACD1所成角的正弦值为( )
如图,在正方体ABCD-A1B1C1D1中,M为BB1的中点,则直线MC与平面ACD1所成角的正弦值为( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{\sqrt{15}}}{5}$ | D. | $\frac{{\sqrt{3}}}{5}$ |
分析 连结B1D,BD,设AC∩BD=O,连结OM,则OM⊥平面ACD1,故而∠MCO为所求角.
解答 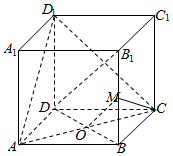 解:连结B1D,BD,设AC∩BD=O,连结OM,
解:连结B1D,BD,设AC∩BD=O,连结OM,
则B1D⊥平面ACD1,OM∥B1D,
∴OM⊥平面ACD1,
∴∠MCO为MC与平面ACD1所成的角,
设正方体棱长为1,则MC=$\sqrt{1+\frac{1}{4}}$=$\frac{\sqrt{5}}{2}$,OM=$\frac{1}{2}$B1D=$\frac{\sqrt{3}}{2}$,
∴sin∠MCO=$\frac{OM}{MC}$=$\frac{\sqrt{15}}{5}$.
故选C.
点评 本题考查了线面角的计算,作出线面角是解题关键,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
20.圆x2+y2-4x+4y-1=0与圆x2+y2+2x-4y+1=0的位置关系是( )
| A. | 相离 | B. | 相交 | C. | 内切 | D. | 外切 |
1.已知向量$\overrightarrow a$与$\overrightarrow b$为单位向量,满足$|\overrightarrow a-3\overrightarrow b|=\sqrt{13}$,则向量$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
20.已知a>b>0且c<d,下列不等式中成立的一个是( )
| A. | a+c>b+d | B. | a-c>b-d | C. | ad<bc | D. | $\frac{a}{c}$>$\frac{b}{d}$ |
