题目内容
9.若关于x 的方程sinx+cosx-m=0在区间[0,$\frac{π}{2}$]上有解,则实数m的取值范围是[1,$\sqrt{2}$].分析 由题意,关于x 的方程sinx+cosx-m=0在区间[0,$\frac{π}{2}$]上有解,转化为函数y=$\sqrt{2}$sin(x+$\frac{π}{4}$)与函数y=m的图象有交点问题.
解答 解:由题意,sinx+cosx-m=0,转化为:sinx+cosx=m,设函数y=$\sqrt{2}$sin(x+$\frac{π}{4}$)
x∈[0,$\frac{π}{2}$]上,则x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{3π}{4}$]
∴sin(x+$\frac{π}{4}$)∈[$\frac{\sqrt{2}}{2},1$]
∴函数y=$\sqrt{2}$sin(x+$\frac{π}{4}$)的值域为[1,$\sqrt{2}$]
关于x 的方程sinx+cosx-m=0在区间[0,$\frac{π}{2}$]上有解,
则函数y=m的值域为[1,$\sqrt{2}$],即m∈[1,$\sqrt{2}$]
故答案为:[1,$\sqrt{2}$].
点评 本题考查了方程有解问题转化为两个函数的交点的问题.属于基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
20.在长为16cm的线段MN上任取一点P,以MP,NP为邻边作一矩形,则该矩形的面积大于60cm2的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
4.若x,y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+2y-3≥0}\\{2x+y-6≤0}\end{array}\right.$,则z=x-2y的最小值为( )
| A. | -6 | B. | -2 | C. | -1 | D. | 3 |
14.已知命题p:?x∈(1,+∞),x3+16>8x,则命题p的否定为( )
| A. | ¬p:?x∈(1,+∞),x3+16≤8x | B. | ¬p:?x∈(1,+∞),x3+16<8x | ||
| C. | ¬p:?x0∈(1,+∞),x03+16≤8x0 | D. | ¬p:?x0∈(1,+∞),x03+16<8x0 |
1.已知集合A={x|x2-x-6≥0},B={x|-3≤x≤3},则A∩B等于( )
| A. | [-3,-2] | B. | [2,3] | C. | [-3,-2]∪{3} | D. | [2,3]∪{-3} |
18.对于实数a>0,“$\frac{1}{x}$<a”是“x>$\frac{1}{a}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.已知k∈R,点P(a,b)是直线x+y=2k与圆x2+y2=k2-2k+3的公共点,则ab的最大值为( )
| A. | 15 | B. | 9 | C. | 1 | D. | -$\frac{5}{3}$ |
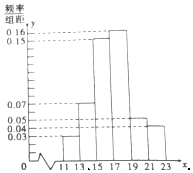 一企业从某生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到的频率分布直方图如图.
一企业从某生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到的频率分布直方图如图.