题目内容
已知a，b是异面直线，
，
分别为取自直线a，b上的单位向量，且
=2
+3
，
=k
-4
，
⊥
，则实数k的值为（ ）
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a |
| b |
| A、-6 | B、6 | C、3 | D、-3 |
考点：空间向量的数量积运算,数量积表示两个向量的夹角
专题：计算题,空间向量及应用
分析：
，
分别为取自直线a，b上的单位向量，且
⊥
，则|
|=|
|=1，
•
=0，运用向量垂直的条件：数量积为0，化简整理，解关于k的方程，即可得到．
| e1 |
| e2 |
| a |
| b |
| e1 |
| e2 |
| e1 |
| e2 |
解答：
解：
，
分别为取自直线a，b上的单位向量，且
⊥
，
则|
|=|
|=1，
•
=0，
•
=2k
2-12
2+（3k-8）
•
=0，
即为2k-12=0，
解得k=6．
故选B．
| e1 |
| e2 |
| a |
| b |
则|
| e1 |
| e2 |
| e1 |
| e2 |
| a |
| b |
| e1 |
| e2 |
| e1 |
| e2 |
即为2k-12=0，
解得k=6．
故选B．
点评：本题主要考查单位向量的定义和向量垂直的条件，考查运算能力，属于基础题．
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
非零向量
和
满足2|
|=|
|，
⊥（
+
），则
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=log
（4-x2）的单调递减区间是（ ）
| 1 |
| 3 |
| A、（-2，0） |
| B、（0，2） |
| C、（-∞，-2） |
| D、（2，+∞） |
如图，四边形ABCD为菱形，ACFE为平行四边形，且平面ACFE⊥平面ABCD，设BD与AC相交于点G，H为FG的中点．如图是某几何体的三视图，则该几何体的体积等于（ ）
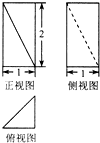
A、
| ||
B、
| ||
| C、1 | ||
D、
|
函数y=log
（x2-3x+2）的单调递增区间为（ ）
| 1 |
| 2 |
| A、（-∞，1） | ||
B、（-∞，
| ||
C、[
| ||
| D、（2，+∞） |